【题目】如图,在△ABC中,AB=AC,AD是角平分线,BE平分∠ABC交AD于点E,点O在AB上,以OB为半径的⊙O经过点E,交AB于点F 
(1)求证:AD是⊙O的切线;
(2)若AC=4,∠C=30°,求 ![]() 的长.
的长.
参考答案:
【答案】
(1)证明:
如图,连接OE,
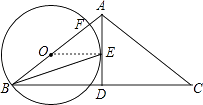
∵OB=OE,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠OBE=∠EBD,
∴∠OEB=∠EBD,
∴OE∥BD,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠OEA=∠BDA=90°,
∴AD是⊙O的切线
(2)解:∵AB=AC=4,∠C=∠B=30°,
∴BD=2 ![]() ,
,
设圆的半径为r,则BO=OE=r,AO=AC﹣OB=4﹣r,
∵OE∥BD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得r=8
,解得r=8 ![]() ﹣12,
﹣12,
∴ ![]() =
= ![]() =
= ![]()
【解析】(1)连接OE,利用角平分线的定义和圆的性质可得∠OBE=∠OEB=∠EBD,可证明OE∥BD,结合等腰三角形的性质可得AD⊥BD,可证得OE⊥AD,可证得AD为切线;(2)利用(1)的结论,结合条件可求得∠AOE=30°,由(1)可知OE∥BD,设半径为r,则OB=OE=r,AO=4﹣r,在Rt△ABD中,由勾股定理可求得BD,由平行线分线段成比例可得到关于r的方程,可求得圆的半径,利用弧长公式可求得 ![]() .
.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)),还要掌握含30度角的直角三角形(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成证明并写出推理根据:
已知,如图,∠1=132°,∠ACB=48°,∠2=∠3.
求证:∠CDB=∠FHB.
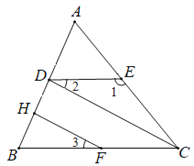
证明:
∵∠1=132°,∠ACB=48° (已知)
∴∠1+∠ACB=180°
∴DE∥BC ( )
∴∠2=∠ ( )
又∵∠2=∠3 (已知)
∴∠3=∠ (等量代换)
∴HF∥DC ( )
∴∠CDB=∠FHB ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校学生进行课外阅读的情况,从全校2200名学生中随机抽取了100名学生,对他们平均每天进行课外阅读的时长进行统计,样本容量是_______.
-
科目: 来源: 题型:
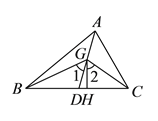
查看答案和解析>>【题目】如图,在
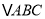 中,
中, 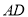 是它的角平分线,
是它的角平分线, 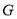 是
是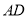 上的一点,
上的一点, 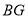 ,
, 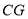 分别平分
分别平分 ,
, 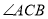 ,
,  ,垂足为点
,垂足为点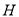 .
.求证:(
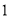 )
)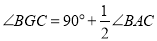 .(
.( )
) .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市2009年元旦的最高气温为12℃,最低气温为-2℃,那么这天的最高气温比最低气温高 ( )
A.-14℃B.-10℃C.14℃D.10℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直径坐标系中,抛物线y=ax2+bx﹣2与x轴交于点A(﹣3,0).B(1,0),与y轴交于点C
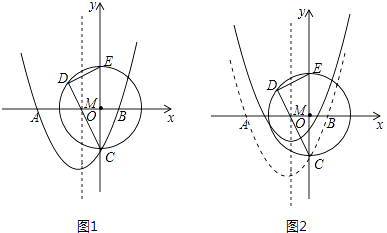
(1)直接写出抛物线的函数解析式;
(2)以OC为半径的⊙O与y轴的正半轴交于点E,若弦CD过AB的中点M,试求出DC的长;
(3)将抛物线向上平移 个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
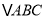 ,
, 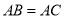 ,
, 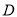 为直线
为直线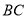 上一点,
上一点, 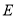 为直线
为直线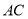 上一点,
上一点, 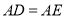 ,设
,设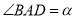 ,
, 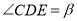 .
.(
 )如图,若点
)如图,若点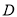 在线段
在线段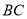 上,点
上,点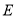 在线段
在线段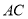 上.
上.①如果
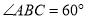 ,
,  ,那么
,那么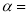 __________,
__________, 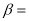 __________.
__________.②求
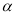 ,
, 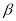 之间的关系式.
之间的关系式.(
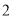 )是否存在不同于以上②中的
)是否存在不同于以上②中的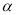 ,
,  之间的关系式?若存在,求出这个关系式,(求出一种不同于②中的关系即可),若不存在,请说明理由.
之间的关系式?若存在,求出这个关系式,(求出一种不同于②中的关系即可),若不存在,请说明理由.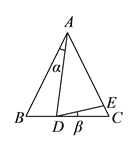
相关试题

