【题目】先化简,再求值:(x﹣1+ ![]() )÷
)÷ ![]() ,其中x的值从不等式组
,其中x的值从不等式组 ![]() 的整数解中选取.
的整数解中选取.
参考答案:
【答案】解:原式=( ![]() +
+ ![]() )÷
)÷ ![]()
= ![]()
![]()
= ![]()
![]()
= ![]() ,
,
解不等式组 ![]() 得:﹣1≤x<
得:﹣1≤x< ![]() ,
,
∴不等式组的整数解有﹣1、0、1、2,
∵分式有意义时x≠±1、0,
∴x=2,
则原式=0.
【解析】整式与分式相加时,整式可看作分母是1的式子,x-1=![]() ,分式的分子出现二次三项式时,可分解因式,x2-3x+2可利用十字相乘法分解为( x 1 ) ( x 2 ),也用求根公式求出可求x2-3x+2=0的根x1=1,x2=2,则x2-3x+2可分为(x-x1)(x-x2)=( x 1 ) ( x 2 ),求分式的值时,取的值一定要使原分式(最起初未化简的式子有意义,即分母不为0)有意义,因此x取2.
,分式的分子出现二次三项式时,可分解因式,x2-3x+2可利用十字相乘法分解为( x 1 ) ( x 2 ),也用求根公式求出可求x2-3x+2=0的根x1=1,x2=2,则x2-3x+2可分为(x-x1)(x-x2)=( x 1 ) ( x 2 ),求分式的值时,取的值一定要使原分式(最起初未化简的式子有意义,即分母不为0)有意义,因此x取2.
【考点精析】掌握一元一次不等式组的整数解是解答本题的根本,需要知道使不等式组中的每个不等式都成立的未知数的值叫不等式组的解,一个不等式组的所有的解组成的集合,叫这个不等式组的解集(简称不等式组的解).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为矩形
为矩形 的对角线,将边
的对角线,将边 沿
沿 折叠,使点
折叠,使点 落在
落在 上的点
上的点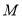 处,将边
处,将边 沿
沿 折叠,使点
折叠,使点 落在
落在 上的点
上的点 处.
处.
(1)求证:四边形
 是平行四边形;
是平行四边形;(2)若
 求四边形
求四边形 的面积及
的面积及 与
与 之间的距离.
之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】为满足市场需求,新生活超市在端午节前夕购进价格为
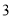 元/个的粽子,根据市场预测,该品牌粽子每个售价
元/个的粽子,根据市场预测,该品牌粽子每个售价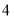 元时,每天能出售
元时,每天能出售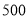 个,并且售价每上涨
个,并且售价每上涨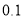 元,其销售量将减少
元,其销售量将减少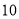 个,为了维护消费者利益,物价部门规定,该品牌粽子的售价不能超过进价的
个,为了维护消费者利益,物价部门规定,该品牌粽子的售价不能超过进价的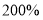 .
.(1)请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为
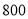 元.
元.(2)定价为多少时每天的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,把不等式组的解集在数轴上表示出来,并求出不等式组的整数解的和.
,把不等式组的解集在数轴上表示出来,并求出不等式组的整数解的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果把一个自然数各数位上的数字从最高位到个位依次排出的一串数字,与从个位到最高位依次排出的一串数字完全相同,那么我们把这样的自然数称为“和谐数”.例如:自然数12321,从最高位到个位排出的一串数字是:1,2,3,2,1,从个位到最高排出的一串数字仍是:1,2,3,2,1,因此12321是一个“和谐数”.再如:22,545,3883,34543,…,都是“和谐数”.
(1)请你直接写出3个四位“和谐数”;请你猜想任意一个四位“和谐数”能否被11整除,并说明理由;
(2)已知一个能被11整除的三位“和谐数”,设其个位上的数字为x(
 ,x为自然数),十位上的数字为y,求y与x的函数关系式.
,x为自然数),十位上的数字为y,求y与x的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点 从点
从点 出发沿
出发沿 方向以
方向以 的速度向点
的速度向点 匀速运动,同时点
匀速运动,同时点 从点
从点 出发沿
出发沿 方向以
方向以 的速度向点
的速度向点 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点 运动的时间是
运动的时间是 .过点
.过点 作
作 于点
于点 连结
连结

(1)求证:
 ;
;(2)四边形
 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的 值,如果不能,说明理由;
值,如果不能,说明理由;(3)当
 为何值时,
为何值时, 为直角三角形?请说明理由.
为直角三角形?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某家电集团公司研制生产的新家电,前期投资
 万元,每生产一台这种新家电,后期还需其他投资
万元,每生产一台这种新家电,后期还需其他投资 万元,已知每台新家电售价为
万元,已知每台新家电售价为  万元,设总投资为
万元,设总投资为 万元(总投资
万元(总投资 前期投资
前期投资 后期投资),总利润为
后期投资),总利润为 万元(总利润
万元(总利润 总售价
总售价 总投资),新家电总产量为
总投资),新家电总产量为 台,(假设可按产量全部卖出)
台,(假设可按产量全部卖出)(1)试用含
 的代数式表示
的代数式表示 和
和 ;
;(2)问新家电总产量超过多少台时,该公司开始盈利?
相关试题

