【题目】如图,正方形ABCD中,E为BC上一点,BE=2CE,连接DE,F为DE中点,以DF为直角边作等腰Rt△DFG,连接BG,将△DFG绕点D顺时针旋转得△DF′G′,G′恰好落在BG的延长线上,连接F′G,若BG=2 ![]() ,则S△GF′G′= .
,则S△GF′G′= . 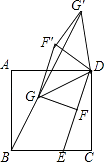
参考答案:
【答案】![]()
【解析】解:如图,作GM⊥BC于M,MG的延长线交AD于N,作DK⊥BG′于K,作KQ⊥DG′于Q,作F′H′BG′于H,BG′交AD于P.
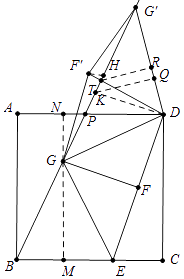
∵BE=2EC,设EC=a,则BE=2a,BC=CD=MN=3a,
∵DG=GE,∠DGE=90°,易证△DGN≌△GEM,设EM=x,
则GN=EM=x,GM=DN=CM=a+x,
∴x+x+a=3a,
∴x=a,
∴BM=EM,∵GM⊥BE,
∴GB=GE=2 ![]() ,
,
∵GM=2a.EM=a,
在Rt△GEM中,可得5a2=20,
∵a>0,
∴a=2,
∴AB=BC=CD=AD=6,GM=4,CM=DN=4,AN=GN=2,DF=EF=GF=G′F′= ![]() ,DG=GE=DG′=2
,DG=GE=DG′=2 ![]() ,
,
∵△GBM∽△BPA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AP=PD=3,
由△APB∽△KPD,可得DK= ![]() ,
,
∵DG′=DG,DK⊥GG′,
∴G′K=GK= ![]() =
= ![]() ,
,
设BG′交DF′于T,作TR⊥DG′于R,
∵tan∠TG′R= ![]() =
= ![]() =
= ![]() ,设TR=3k,RG′=4k,
,设TR=3k,RG′=4k,
∵∠TDR=45°,
∴TR=DR=3k,
∴7k=2 ![]() ,
,
∴k= ![]() ,
,
∴TG′=5k= ![]() ,
,
由△′F′H∽△G′TF′,
可得G′H= ![]() ,
,
在Rt△G′F′H中,F′H= ![]() =
= ![]() ,
,
∴S△GG′F′= ![]() GG′F′H=
GG′F′H= ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
所以答案是 ![]() .
.
【考点精析】关于本题考查的等腰直角三角形和勾股定理的概念,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】襄江中学组织九年级部分学生到古隆中参观,租用的客车有50座和30座两种可供选择.学校根据参加参观的学生人数计算可知:若只租用30座客车x辆,还差10人才能坐满;若只租用50座客车,比只租用30座客车少用2辆,且有一辆车没有坐满但超过30人.
(1)写出九年级参观的学生人数y与x的关系式;
(2)求出此次参观的九年级学生人数;
(3)若租用一辆30座客车往返费用为260元,租用一辆50座客车往返费用为400元,如何选择租车方案费用最低? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中有三点
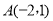 、
、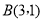 、
、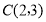 ,请回答如下问题:
,请回答如下问题:(1)在坐标系内描出点
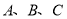 的位置:
的位置:(2)求出以
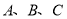 三点为顶点的三角形的面积;
三点为顶点的三角形的面积;(3)在
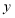 轴上是否存在点
轴上是否存在点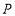 ,使以
,使以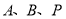 三点为顶点的三角形的面积为10,若存在,请直接写出点
三点为顶点的三角形的面积为10,若存在,请直接写出点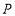 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从A、B两地同时出发匀速相向而行,大楼C位于AB之间,甲与乙相遇在AC中点处,然后两车立即掉头,以原速原路返回,直到各自回到出发点.设甲、乙两车距大楼C的距离之和为y(千米),甲车离开A地的时间为t(小时),y与t的函数图象所示,则第21小时时,甲乙两车之间的距离为千米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图10,在平面直角坐标系中,点
 的坐标分别为
的坐标分别为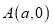 ,
,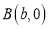 ,且
,且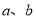 满足
满足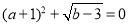 .现同时将点
.现同时将点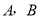 分别向上平移2个单位,再向右平移1个单位,分别得到点
分别向上平移2个单位,再向右平移1个单位,分别得到点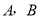 的对应点
的对应点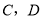 ,连接
,连接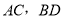 得
得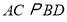 .
.(1)直接写出点
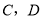 的坐标和四边形
的坐标和四边形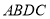 的面积;
的面积;(2)若在坐标轴上存在点
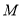 ,使
,使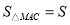 四边形
四边形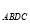 ,求出点
,求出点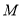 的坐标;
的坐标;(3)若点
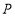 在直线
在直线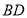 上运动,连接
上运动,连接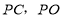 .请画出图形,写出
.请画出图形,写出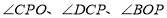 的数量关系并证明.
的数量关系并证明.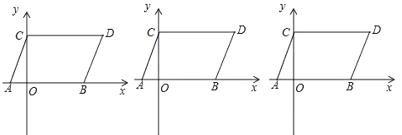
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)2a+3(a2-b)-2(2a2+a-
 b),其中a=
b),其中a= ,b=-2;
,b=-2;(2)(m-5n+4mn)-2(2m-4n+6mn),其中m-n=4,mn=-3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间为了改变管理松懈的状况,准备采取每天任务定额和超产有奖的措施,从而提高工作效率.下面是该车间15名工人过去一天中各自装配机器的数量(单位:台):
15,6,16,7,15,8,7,13,8,11,8,10,9,10,9.
请回答下列问题:
(1)这组数据的平均数、众数和中位数各是多少(结果精确到0.01台)?
(2)管理者应确定每人标准日产量为多少台比较合适?
相关试题

