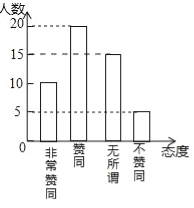
【题目】二孩子政策的落实引起了全社会的关注,某校学生数学兴趣小组为了了解本校同学父母生育二孩子的态度,在学校抽取了部分同学对父母生育二孩子所持的态度进行了问卷调查,调查分别为非常赞同、赞同、无所谓、不赞同等四种态度,现将调查统计结果制成了如图两幅统计图,请结合两幅统计图,回答下列问题:

(1)在这次问卷调查中一共抽取了__________名学生,a=________%;
(2)请补全条形统计图;
(3)持“不赞同”态度的学生人数的百分比所占扇形的圆心角为__________度;
(4)若该校有3000名学生,请你估计该校学生对父母生育二孩子持“赞同”和“非常赞同”两种态度的人数之和.
参考答案:
【答案】(1)50,37.5%;(2)详见解析;(3)36°;(4)1800.
【解析】试题分析:(1)由赞同的人数除以赞同的人数所占的百分比,即可求出样本容量,再求出无所谓态度的人数,进而求出a的值;(2)由(1)可知无所谓态度的人数,将条形统计图补充完整即可;(3)求出不赞成人数的百分数,即可求出圆心角的度数;(4)求出“赞同”和“非常赞同”两种态度的人数所占的百分比,用样本估计总体的思想计算即可.
试题解析:(1)20÷40%=50(人),无所谓态度的人数为50﹣10﹣20﹣5=15,则a=![]() ×100%=37.5%;
×100%=37.5%;
(2)补全条形统计图如图所示:
(3)不赞成人数占总人数的百分数为![]() ×100%=10%,
×100%=10%,
持“不赞同”态度的学生人数的百分比所占扇形的圆心角为10%×360°=36°,
(4)“赞同”和“非常赞同”两种态度的人数所占的百分数为![]() ×100%=60%,
×100%=60%,
则该校学生对父母生育二孩持“赞同”和“非常赞同”两种态度的人数之和为3000×60%=1800人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
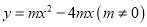 与x轴交于A,B两点(点A在点B的左侧).
与x轴交于A,B两点(点A在点B的左侧).(1)求点A,B的坐标及抛物线的对称轴;
(2)过点B的直线l与y轴交于点C,且
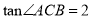 ,直接写出直线l的表达式;
,直接写出直线l的表达式;(3)如果点
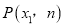 和点
和点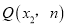 在函数
在函数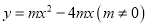 的图象上,PQ=2a且
的图象上,PQ=2a且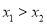 , 求
, 求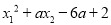 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD的一条对角线长为6,边AB的长是方程x2-7x+12=0的一个根,则菱形ABCD的周长为( )
A. 12 B. 14 C. 16 D. 24
-
科目: 来源: 题型:
查看答案和解析>>【题目】补全下列推理过程:
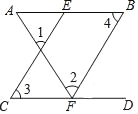
如图,已知∠1=∠2,∠3=∠4,试说明AB∥CD.
解:∵∠1=∠2(已知)
∴CE∥FB ( )
∴∠4=∠AEC ( )
∵∠3=∠4 ( 已知)
∴∠3=∠AEC ( )
∴AB∥CD( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接G20杭州峰会的召开,某校八年级(1)(2)班准备集体购买一种T恤衫参加一项社会活动.了解到某商店正好有这种T恤衫的促销,当购买10件时每件140元,购买数量每增加1件单价减少1元;当购买数量为60件(含60件)以上时,一律每件80元.
(1)如果购买x件(10<x<60),每件的单价为y元,请写出y关于x的函数关系式;
(2)如果八(1)(2)班共购买了100件T恤衫,由于某种原因需分两批购买,且第一批购买数量多于30件且少于60件.已知购买两批T恤衫一共花了9200元,求第一批T恤衫的购买数量. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x2﹣2x﹣8=0.解决以下问题:
(1)请按要求分别解这个方程:①配方法;②因式分解法.
(2)这些方法都是将解方程转化为解方程,以达到将方程降次的目的;
(3)尝试解方程:x3+2x2﹣3x=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.某一事件发生的可能性非常大就是必然事件
B.2020年1月27日杭州会下雪是随机事件
C.概率很小的事情不可能发生
D.投掷一枚质地均匀的硬币1000次,正面朝上的次数一定是500次
相关试题

