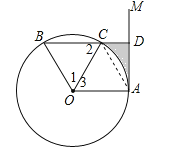
【题目】如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
(1)求证:AM是⊙O的切线;
(2)若DC=2,求图中阴影部分的面积.(结果保留π和根号)

参考答案:
【答案】(1)答案见解析;(2)![]() .
.
【解析】试题分析:(1)由已知条件得到△BOC是等边三角形,根据等边三角形的性质得到∠1=∠2=60°,由角平分线的性质得到∠1=∠3,根据平行线的性质得到∠OAM=90°,于是得到结论;
(2)根据等边三角形的性质得到∠OAC=60°,根据三角形的内角和得到∠CAD=30°,根据勾股定理得到AD的长,于是得到结论.
(1)∵∠B=60°,∴△BOC是等边三角形,∴∠1=∠2=60°,∵OC平分∠AOB,∴∠1=∠3,∴∠2=∠3,∴OA∥BD,∴∠BDM=90°,∴∠OAM=90°,∴AM是⊙O的切线;
(2)∵∠3=60°,OA=OC,∴△AOC是等边三角形,∴∠OAC=60°,∵∠OAM=90°,∴∠CAD=30°,∵CD=2,∴AC=2CD=4,∴AD=![]() ,∴S阴影=S梯形OADC﹣S扇形OAC=
,∴S阴影=S梯形OADC﹣S扇形OAC=![]() (4+2)×
(4+2)×![]() ﹣
﹣![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】以下是推导“三角形内角和定理”的学习过程,请补全证明过程及推理依据.

已知:如图,△ABC.
求证:∠A+∠B+∠C=180°.
证明:过点A作DE∥BC,(请在图上画出该辅助线并标注D,E两个字母)
∠B=∠BAD,∠C= .( )
∵点D,A,E在同一条直线上,
∴ (平角的定义)
∴∠B+∠BAC+∠C=180°
即三角形的内角和为180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,随着电子商务的快速发展,电商包裹件总量占当年快递件总量的比例逐年增长.根据某快递公司某网点的数据统计,得到如下统计表:

(1)直接写出m,n的值,并在图中画出电商包裹件总量占快递件总量百分比的折线统计图;
(2)若2019年该网点快递件总量预计达到7万件,请根据图表信息,估计2019年电商包裹件总量约为多少万件?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC的平分线交AC于点D.作∠BDE=∠ABD交AB于点E.

(1)求证:ED∥BC;
(2)点M为射线AC上一点(不与点A重合)连接BM,∠ABM的平分线交射线ED于点N.若∠MBC=
 ∠NBC,∠BED=105°,求∠ENB的度数.
∠NBC,∠BED=105°,求∠ENB的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A点的坐标为(1,0).以OA为边在x轴上方画一个正方形OABC.以原点O为圆心,正方形的对角线OB长为半径画弧,与x轴正半轴交于点D.

(1)点D的坐标是 ;
(2)点P(x,y),其中x,y满足2x-y=-4.
①若点P在第三象限,且△OPD的面积为3
 ,求点P的坐标;
,求点P的坐标;②若点P在第二象限,判断点E(
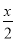 +1,0)是否在线段OD上,并说明理由.
+1,0)是否在线段OD上,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
相关试题

