【题目】如图,在平面直角坐标系xOy中,A点的坐标为(1,0).以OA为边在x轴上方画一个正方形OABC.以原点O为圆心,正方形的对角线OB长为半径画弧,与x轴正半轴交于点D.

(1)点D的坐标是 ;
(2)点P(x,y),其中x,y满足2x-y=-4.
①若点P在第三象限,且△OPD的面积为3![]() ,求点P的坐标;
,求点P的坐标;
②若点P在第二象限,判断点E(![]() +1,0)是否在线段OD上,并说明理由.
+1,0)是否在线段OD上,并说明理由.
参考答案:
【答案】(1)(![]() ,0);(2)①P(-5,-6);②点E在线段OD上,见解析.
,0);(2)①P(-5,-6);②点E在线段OD上,见解析.
【解析】
(1)先求出正方形的边长,再用勾股定理求出OB,即可得出结论;
(2)①先表示出PQ,再利用△ODP的没解决建立方程求解,即可得出结论;
②根据点P在第二象限,求出x的范围,进而判断出点E在x轴正半轴上,即可得出结论.
(1)∵四边形OABC是正方形,且A(1,0),
∴OA=AB=1,
根据勾股定理得,OB=![]() ,
,
∴OD=![]() ,
,
∴D(![]() ,0),
,0),
故答案为:(![]() ,0);
,0);
(2)①如图,过点P作PQ⊥x轴于点Q,
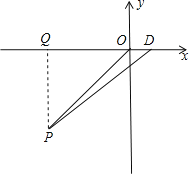
∵点P在第三象限,
∴y=2x+4<0,
∴PQ=-(2x+4),
∵D(![]() ,0),
,0),
∴OD=![]() ,
,
∴S△ODP=![]() ODPQ=3
ODPQ=3![]() ,
,
即:-![]() ×
×![]() ×(2x+4)=3
×(2x+4)=3![]() ,
,
∴x=-5,
∴P(-5,-6);
②点E在线段OD上,
理由:∵2x-y=-4,
∴y=2x+4,
∵点P在第二象限,
∴![]() ,
,
∴-2<x<0,
∴0<![]() x+1<1,
x+1<1,
∴点E在x轴正半轴上,
∵点D在x轴正半轴,OD=![]() ,
,
∴0<OE<OD,
∴点E在线段OD上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,随着电子商务的快速发展,电商包裹件总量占当年快递件总量的比例逐年增长.根据某快递公司某网点的数据统计,得到如下统计表:

(1)直接写出m,n的值,并在图中画出电商包裹件总量占快递件总量百分比的折线统计图;
(2)若2019年该网点快递件总量预计达到7万件,请根据图表信息,估计2019年电商包裹件总量约为多少万件?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
(1)求证:AM是⊙O的切线;
(2)若DC=2,求图中阴影部分的面积.(结果保留π和根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC的平分线交AC于点D.作∠BDE=∠ABD交AB于点E.

(1)求证:ED∥BC;
(2)点M为射线AC上一点(不与点A重合)连接BM,∠ABM的平分线交射线ED于点N.若∠MBC=
 ∠NBC,∠BED=105°,求∠ENB的度数.
∠NBC,∠BED=105°,求∠ENB的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度,随机抽取了部分学生进行调查(每人限选1项),现将调查结果绘制成如下两幅不完整的统计图,根据图中所给的信息解答下列问题.

(1)喜爱动画的学生人数和所占比例分别是多少?
(2)请将条形统计图补充完整;
(3)若该校共有学生1000人,依据以上图表估计该校喜欢体育的人数约为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(操作发现)
如图 1,在边长为 1 个单位长度的小正方形组成的网格中,ABC 的三个顶点均在格点上.现将ABC 绕点 A 按顺时针方向旋转 90°,点 B 的对应点为 B′,点 C 的对应点为 C′, 连接 BB′,如图所示则∠AB′B= .
(2)(解决问题)
如图 2,在等边ABC 内有一点 P,且 PA=2,PB=
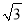 ,PC=1,如果将△BPC 绕点 B 顺时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;
,PC=1,如果将△BPC 绕点 B 顺时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;(3)(灵活运用)
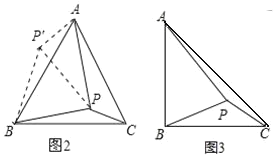
如图 3,将(2)题中“在等边ABC 内有一点 P 改为“在等腰直角三角形 ABC 内有一点P”,且 BA=BC,PA=6,BP=4,PC=2,求∠BPC 的度数.

相关试题

