【题目】如图,在平面直角坐标系中,圆M经过原点O,且与x轴、y轴分别相交于A(﹣8,0),B(0,﹣6)两点. 
(1)求出直线AB的函数解析式;
(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交x轴于D、E两点,在抛物线上是否存在点P,使得S△PDE= ![]() S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:设直线AB的函数解析式为y=kx+b,
把A(﹣8,0),B(0,﹣6)代入得 ![]() ,解得
,解得  ,
,
所以直线AB的解析式为y=﹣ ![]() x﹣6
x﹣6
(2)解:在Rt△AOB中,AB= ![]() =10,
=10,
∵∠AOB=90°,
∴AB为⊙M的直径,
∴点M为AB的中点,M(﹣4,﹣3),
∵MC∥y轴,MC=5,
∴C(﹣4,2),
设抛物线的解析式为y=a(x+4)2+2,
把B(0,﹣6)代入得16a+2=﹣6,解得a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() (x+4)2+2,即y=﹣
(x+4)2+2,即y=﹣ ![]() x2﹣4x﹣6
x2﹣4x﹣6
(3)解:存在.
当y=0时,﹣ ![]() (x+4)2+2=0,解得x1=﹣2,x2=﹣4,
(x+4)2+2=0,解得x1=﹣2,x2=﹣4,
∴D(﹣6,0),E(﹣2,0),
S△ABC=S△ACM+S△BCM= ![]() 8CM=20,
8CM=20,
设P(t,﹣ ![]() t2﹣4t﹣6),
t2﹣4t﹣6),
∵S△PDE= ![]() S△ABC,
S△ABC,
∴ ![]() (﹣2+6)|﹣
(﹣2+6)|﹣ ![]() t2﹣4t﹣6|=
t2﹣4t﹣6|= ![]() 20,
20,
即|﹣ ![]() t2﹣4t﹣6|=1,
t2﹣4t﹣6|=1,
当﹣ ![]() t2﹣4t﹣6=1,解得t1=﹣4+
t2﹣4t﹣6=1,解得t1=﹣4+ ![]() ,t2=﹣4﹣
,t2=﹣4﹣ ![]() ,此时P点坐标为(﹣4+
,此时P点坐标为(﹣4+ ![]() ,1)或(﹣4﹣
,1)或(﹣4﹣ ![]() ,0)
,0)
当﹣ ![]() t2﹣4t﹣6=﹣1,解得t1=﹣4+,t2=﹣4﹣
t2﹣4t﹣6=﹣1,解得t1=﹣4+,t2=﹣4﹣ ![]() ;此时P点坐标为(﹣4+
;此时P点坐标为(﹣4+ ![]() ,﹣1)或(﹣4﹣
,﹣1)或(﹣4﹣ ![]() ,0)
,0)
综上所述,P点坐标为(﹣4+ ![]() ,1)或(﹣4﹣
,1)或(﹣4﹣ ![]() ,0)或(﹣4+
,0)或(﹣4+ ![]() ,﹣1)或(﹣4﹣
,﹣1)或(﹣4﹣ ![]() ,0)时,使得S△PDE=
,0)时,使得S△PDE= ![]() S△ABC.
S△ABC.

【解析】(1)利用待定系数法可求出直线AB的解析式;(2)先利用勾股定理计算出AB=10,再根据圆周角定理得到AB为⊙M的直径,则点M为AB的中点,M(﹣4,﹣3),则可确定C(﹣4,2),然后利用顶点式求出抛物线解析式;(3)通过解方程﹣ ![]() (x+4)2+2=0得到D(﹣6,0),E(﹣2,0),利用S△ABC=S△ACM+S△BCM , 可求出S△ABC=10,设P(t,﹣
(x+4)2+2=0得到D(﹣6,0),E(﹣2,0),利用S△ABC=S△ACM+S△BCM , 可求出S△ABC=10,设P(t,﹣ ![]() t2﹣4t﹣6),所以
t2﹣4t﹣6),所以 ![]() (﹣2+6)|﹣
(﹣2+6)|﹣ ![]() t2﹣4t﹣6|=
t2﹣4t﹣6|= ![]() 20,然后解绝对值方程求出t即可得到P点坐标.
20,然后解绝对值方程求出t即可得到P点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN,MC交于点E,直线BM,CN交于点F.
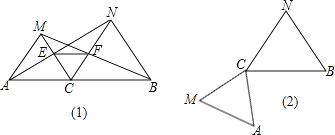
(1)求证:AN=MB;
(2)求证:△CEF为等边三角形;
(3)将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在(2)中画出符合要求的图形,并判断(1)(2)题中的两结论是否依然成立.并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC、BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.则不能使四边形ABCD成为矩形的是( )
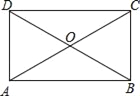
A. ①②③ B. ②③④ C. ②⑤⑥ D. ④⑤⑥
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形OABC在平面直角坐标系中如图,已知AB=10,BC=8,EB是C上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=
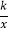 (k>0)与AB相交于点F,则线段AF的长为( )
(k>0)与AB相交于点F,则线段AF的长为( )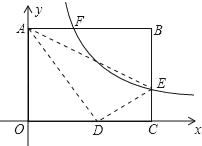
A.
 B.
B. 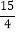 C. 2 D.
C. 2 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
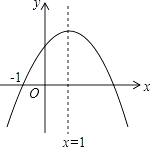
A.ac>0
B.当x>1时,y随x的增大而增大
C.2a+b=1
D.方程ax2+bx+c=0有一个根是x=3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABO中,AB⊥OB,OB=
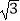 ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为( )
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为( ) 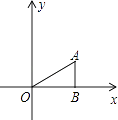
A.(﹣1,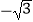 )
)
B.(﹣1,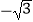 )或(﹣2,0)
)或(﹣2,0)
C.(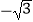 ,﹣1)或(0,﹣2)
,﹣1)或(0,﹣2)
D.(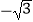 ,﹣1)
,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】
 月读书节,深圳市为统计某学校初三学生读书状况,如下图:
月读书节,深圳市为统计某学校初三学生读书状况,如下图: 月读书节,深圳市为统计某学校初三学生读书状况,如下图:
月读书节,深圳市为统计某学校初三学生读书状况,如下图: 三本以上的
三本以上的 值为________,参加调查的总人数为________,补全统计图;
值为________,参加调查的总人数为________,补全统计图; 三本以上的圆心角为________.
三本以上的圆心角为________. 全市有
全市有 万学生,三本以上有________人.
万学生,三本以上有________人.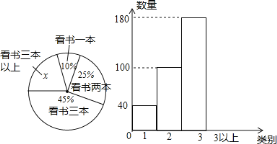
相关试题

