【题目】定义:任意两个数a,b,按规则c=![]() a+b得到一个新数c,称所得的新数c为数a,b的“传承数。”
a+b得到一个新数c,称所得的新数c为数a,b的“传承数。”
(1)若a=1,b=2,求a,b的“传承数”c;
(2)若a=1,b=![]() ,且
,且![]() +3x+1=0,求a,b的“传承数”c;
+3x+1=0,求a,b的“传承数”c;
(3)若a=2n+1,b=n1,且a,b的“传承数”c值为一个整数,则整数n的值是多少?
参考答案:
【答案】(1)![]() ;(2)c=6;(3)n为2、0、2或4.
;(2)c=6;(3)n为2、0、2或4.
【解析】
(1)根据题目中的定义可以求得当a=-1,b=2时,a,b的“传承数”c;
(2)根据题目中定义,可以求得相应的传承数;
(3)根据题意和题目中的定义,可以求得整数n的值.
(1)∵a=-1,b=2
∴c=![]() -a+b=-
-a+b=-![]() -(-1)+2=
-(-1)+2=![]() ;
;
(2)∵![]() +3x+1=0
+3x+1=0
∴x≠0,两边同时除以x得:x+3+![]() =0
=0
∴x+![]() =3
=3
∵a=1,b=![]()
∴c=![]() -a+b=
-a+b=![]() -1+
-1+![]() =
=![]() +2+
+2+![]() -3=
-3=![]() -3=
-3=![]() -3=9-3=6;
-3=9-3=6;
(3)∵a=2n+1,b=n-1
∴c=![]() -a+b=2n+1n-1-(2n+1)+n-1=2n-2+3n-1-n-2=2+3n-1-n-2=3n-1-n
-a+b=2n+1n-1-(2n+1)+n-1=2n-2+3n-1-n-2=2+3n-1-n-2=3n-1-n
∵c为整数,n为整数∴n-1为-3、-1、1或3
∴n为-2、0、2或4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ,
, ,
, ,
, 平分
平分

(1)说明:
 ;(2)求
;(2)求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+3(k<0)分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒.
(1)当k=-1时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).
①直接写出t=1秒时C、Q两点的坐标;
②若以Q、C、A为顶点的三角形与△AOB相似,求t的值.
(2)当k=
 时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),
时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),①求CD的长;
②设△COD的OC边上的高为h,当t为何值时,h的值最大?


-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂有新、旧两台机器,上半年,新机器平均每天比旧机器多生产50件产品,新机器生产600件产品所用的时间与旧机器生产450件产品所用的时间相同.
(1)求上半年新、旧机器日均产品数;
(2)下半年,新机器提高了生产效率,而旧机器由于不断损耗,生产效率降低,经测算,新机器日均产品数提高的百分数是旧机器日均产品数降低的百分数的2倍,结果新机器生产960件产品所用的时间与旧机器生产540件产品所用的时间相同,求新机器日均产品比旧机器多多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对任意一个三位数
 ,如果
,如果 满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为
满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为 .例如
.例如 ,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以
,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以 .
.(1)计算:
 和
和 ;
;(2)若
 是“相异数”,证明:
是“相异数”,证明: 等于
等于 的各数位上的数字之和.
的各数位上的数字之和. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E为矩形ABCD的边AB上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,若BE=1,BC=3,则CD的长为( )

A.5B.6C.4D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知抛物线
 与x轴交于A,B两点,与y轴交于点C,顶点为D,点C’是点C关于对称轴的对称点,过点D作DG⊥x轴交x轴于点G,交线段AC于点E。
与x轴交于A,B两点,与y轴交于点C,顶点为D,点C’是点C关于对称轴的对称点,过点D作DG⊥x轴交x轴于点G,交线段AC于点E。(1)连接DC,求△DCE的周长;
(2)如图2,点P是线段AC上方抛物线上的一点,过P作PH⊥x 轴交x轴于点H,交线段AC于点Q,当四边形PCQC’的面积最大时,在线段PH上有一动点M,在线段DG上有一动点N,在y轴上有一动点E,且满足MN⊥PH,连接AM,MN,NE,DE,求AM+MN+NE+DE的最小值;
(3)如图3,将抛物线沿直线AC进行平移,平移过程中的点D记为D’,点C记为C’,连接D’C’所形成的直线与x轴相交于点G,请问是否存在这样的点G,使得△D’OG为等腰三角形?若存在,求出此时OG的长度,若不存在,请说明理由。


图1 图2
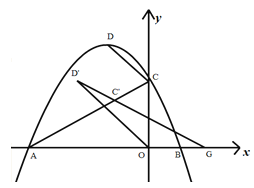
图3
相关试题

