【题目】如图,在正方形![]() 中,过
中,过![]() 作一直线与
作一直线与![]() 相交于点
相交于点![]() ,过
,过![]() 作
作![]() 垂直
垂直![]() 于点
于点![]() ,过
,过![]() 作
作![]() 垂直
垂直![]() 于点
于点![]() ,在
,在![]() 上截取
上截取![]() ,再过
,再过![]() 作
作![]() 垂直
垂直![]() 交
交![]() 于
于![]() .若
.若![]() .则
.则![]() 与四边形
与四边形![]() 的面积之和为________.
的面积之和为________.

参考答案:
【答案】9
【解析】
由ABCD为正方形,根据正方形的性质得到AB=BC,∠ABC=90°,即∠CBG+∠ABF=90°,又根据CG与BE垂直得到∠BCG+∠CBG=90°,根据同角的余角相等得到一对角相等,又根据一对直角相等,利用“AAS”即可得到三角形BCG与三角形FBA全等,根据全等三角形的对应边相等得到AF与BG相等,又因为FH=FB,从而得到AH=FG,然后由垂直得到一对直角相等,加上一个公共角,得到三角形APH与三角形ABF相似,根据相似得比例,设AH=FG=x,用x表示出PH,由四边形PHFB一组对边平行,另一组对边不平行得到此四边形为梯形,根据梯形的面积公式,由上底PH,下底为BF=3,高FH=3,表示出梯形的面积;然后在三角形BCG与三角形ECG中,根据同角的余角相等,再加上一对直角得到两三角形相似,根据相似得比例,用含x的式子表示出GE,由CG=3,表示出的GE,利用三角形的面积公式表示出直角三角形CGE的面积,把表示出的两面积相加,化简即可得到结论.
∵四边形ABCD为正方形,∴AB=BC,∠ABC=90°,即∠CBG+∠ABF=90°,又CG⊥BE,即∠BGC=90°,∴∠BCG+∠CBG=90°,∴∠ABF=∠BCG,又AF⊥BG,∴∠AFB=∠BGC=90°,∴△ABF≌△BCG,∴AF=BG,BF=CG=FH=3.
又∵FH=BF,∴AH=FG,设AH=FG=x.
∵PH⊥AF,BF⊥AF,∴∠AHP=∠AFB=90°,又∠PAH为公共角,∴△APH∽△ABF,∴![]() =
=![]() ,即PH=
,即PH=![]() .
.
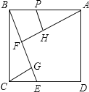
∵PH∥BF,BP不平行FH,∴四边形BFHP为梯形,其面积为![]() =
=![]() +
+![]() ;
;
又∵∠BCG+∠ECG=90°,∠ECG+∠BEC=90°,∴∠BCG=∠BEC,又∠BGC=∠CGE=90°,∴△BCG∽△CEG,∴![]() =
=![]() ,即GE=
,即GE=![]() ,故Rt△CGE的面积为
,故Rt△CGE的面积为![]() ×3×
×3×![]() ,则△CGE与四边形BFHP的面积之和为
,则△CGE与四边形BFHP的面积之和为![]() +
+![]() +
+![]() =
=![]() +
+![]() =9.
=9.
故答案为:9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABE中,∠BAE=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )

A. 45°B. 60°C. 50°D. 55°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车4S店销售某种型号的汽车,每辆进货价为15万元,该店经过一段时间的市场调研发现:当销售价为25万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出1辆.该4S店要想平均每周的销售利润为90万元,并且使成本尽可能的低,则每辆汽车的定价应为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于y轴对称的△ABlCl;
(2)点P在x轴上,且点P到点B与点C的距离之和最小,直接写出点P的坐标为______.

-
科目: 来源: 题型:
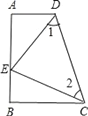
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠B=90°,E是AB上一点,且AE=BC,∠1=∠2.
(1)证明:AB=AD+BC;
(2)判断△CDE的形状?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 中,
中, ,
, ,点
,点 为
为 的中点.如果点
的中点.如果点 在线段
在线段 上以
上以 的速度由点
的速度由点 向
向 点运动,同时,点
点运动,同时,点 在线段
在线段 上由点
上由点 向
向 点运动.
点运动.
(1)若点
 的运动速度与点
的运动速度与点 的运动速度相等,经过1秒后,
的运动速度相等,经过1秒后, 与
与 是否全等,请说明理由.
是否全等,请说明理由.(2)若点
 的运动速度与点
的运动速度与点 的运动速度不相等,当点
的运动速度不相等,当点 的运动速度为多少时,能够使
的运动速度为多少时,能够使 与
与 全等?
全等? -
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明的袋子中装有
 个相同小球,分别标有不等的自然数
个相同小球,分别标有不等的自然数 、
、 、
、 、
、 ,小丽每次从袋中同时摸出
,小丽每次从袋中同时摸出 个小球,并计算摸出的这
个小球,并计算摸出的这 个小球上数字之和,记录后将小球放回袋中搅匀,进行重复实验.实验数据如下表:
个小球上数字之和,记录后将小球放回袋中搅匀,进行重复实验.实验数据如下表:摸球总次数

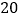








“和为
 ”出现的频数
”出现的频数




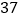



“和为
 ”出现的频率
”出现的频率









 如果实验继续进行下去,出现“和为
如果实验继续进行下去,出现“和为 ”的频率将稳定在它的概率附近.试估计出现“和为
”的频率将稳定在它的概率附近.试估计出现“和为 ”的概率;
”的概率; 根据
根据 中结论,求出自然数
中结论,求出自然数 的值.
的值.
相关试题

