【题目】如图,在矩形ABCD中,AB=6,AD=8,矩形内一动点P使得S△PAD=![]() S矩形ABCD,则点P到点A、D的距离之和PA+PD的最小值为_____.
S矩形ABCD,则点P到点A、D的距离之和PA+PD的最小值为_____.

参考答案:
【答案】8![]()
【解析】
根据S△PAD=![]() S矩形ABCD,得出动点P在与AD平行且与AD的距离是4的直线l上,作A关于直线l的对称点E,连接DE,BE,则DE的长就是所求的最短距离.然后在直角三角形ADE中,由勾股定理求得DE的值,即可得到PA+PD的最小值.
S矩形ABCD,得出动点P在与AD平行且与AD的距离是4的直线l上,作A关于直线l的对称点E,连接DE,BE,则DE的长就是所求的最短距离.然后在直角三角形ADE中,由勾股定理求得DE的值,即可得到PA+PD的最小值.
设△PAD中AD边上的高是h.
∵S△PAD=![]() S矩形ABCD,
S矩形ABCD,
∴![]() ADh=
ADh=![]() ADAB,
ADAB,
∴h=![]() AB=4,
AB=4,
∴动点P在与AD平行且与AD的距离是4的直线l上,
如图,作A关于直线l的对称点E,连接BE,DE,则DE的长就是所求的最短距离.

在Rt△ADE中,∵AD=8,AE=4+4=8,
DE=![]() ,
,
即PA+PD的最小值为8![]() .
.
故答案8![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某空调厂的装配车间原计划用2个月时间(每月以30天计算),每天组装150台空调.
(1)从组装空调开始,每天组装的台数 m(单位:台/天)与生产的时间 t(单位:天)之间有怎样的函数关系?
(2)由于气温提前升高、厂家决定这批空调提前十天上市,那么装配车间每天至少要组装多少空调?
-
科目: 来源: 题型:
查看答案和解析>>【题目】西南大学附中初2020级小李同学想利用学过的知识测量棵树的高度,假设树是竖直生长的,用图中线段AB表示,小李站在C点测得∠BCA=45°,小李从C点走4米到达了斜坡DE的底端D点,并测得∠CDE=150°,从D点上斜坡走了8米到达E点,测得∠AED=60°,B,C,D在同一水平线上,A、B、C、D、E在同一平面内,则大树AB的高度约为( )米.(结果精确到0.1米,参考数据:
 ≈1.41,
≈1.41, ≈1.73)
≈1.73)
A.24.3B.24.4C.20.3D.20.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=a(x+
 )2+k(a>0),点A(﹣4,y1)、B(﹣2,y2)、C(2,y3)是图象上的三个点,则y1、y2、y3的大小关系是_____(用“<”连接).
)2+k(a>0),点A(﹣4,y1)、B(﹣2,y2)、C(2,y3)是图象上的三个点,则y1、y2、y3的大小关系是_____(用“<”连接). -
科目: 来源: 题型:
查看答案和解析>>【题目】探究:如图①,在
 中,点
中,点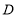 ,
,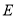 ,
, 分别是边
分别是边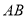 ,
,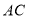 ,
,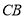 上,且
上,且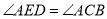 ,
,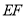 ∥
∥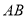 ,若
,若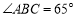 ,求
,求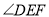 的度数.请把下面的解答过程补充完整.(请在空上填写推理依据或数学式子)
的度数.请把下面的解答过程补充完整.(请在空上填写推理依据或数学式子)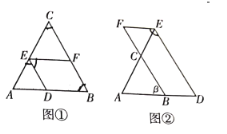
解:∵
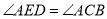
∴
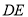 ∥
∥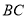 (_____________________________)
(_____________________________)∴
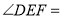 ____________(_______________________)
____________(_______________________)∵
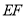 ∥
∥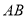
∴_________
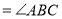 (_____________________)
(_____________________)∴
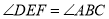
∵
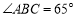
∴
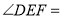 _____________
_____________应用:如图②,在
 中,点
中,点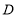 ,
,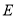 ,
, 分别是边
分别是边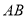 ,
,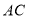 ,
,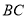 的延长线上,且
的延长线上,且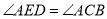 ,
,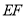 ∥
∥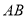 ,若
,若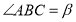 ,则
,则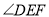 的大小为_____________(用含
的大小为_____________(用含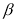 的代数式表示).
的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB两港航程为75.2km,快艇从A港出发顺流匀速驶向B港,同时一艘小船从B港出发逆流匀速驶向A港(小船到达A港后就停止航行),行至某刻快艇发现有重要货物忘带,立刻原路返回A港口装载(装货时间忽略不计),然后继续顺流驶向B港,到达B港后又逆流匀速返回A港,若快艇和小船在静水中都保持各自速度不变两船之间的距离y(km)与行驶时间x(min)之间的函数图象如图所示,则两船第二次相遇时的地点与B港口相距_____km.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校锅炉旁建有一个储煤库,开学初购进一批煤,现在知道:按每天用煤0.6吨计算,一学期(按150天计算)刚好用完.若每天的耗煤量为 x吨,那么这批煤能维持 y天.
(1)则 y与 x之间有怎样的函数关系?
(2)画出此函数的图象.
(3)若每天节约0.1吨,则这批煤能多维持多少天?
相关试题

