【题目】如图,△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论:(1)AD上任意一点到点C、D的距离相等;(2)AD上任意一点到AB、AC的距离相等;(3)AD⊥BC且BD=CD;(4)∠BDE=∠CDF,其中正确的个数是( )

A. 1个B. 2个C. 3个D. 4个
参考答案:
【答案】D
【解析】
试题先根据等腰三角形三线合一的性质得出AD是BC的中垂线,再由中垂线的性质可判断①正确;
根据角平分线的性质可判断②正确;
根据等腰三角形三线合一的性质得出AD是BC的中垂线,从而可判断③正确;
根据△BDE和△DCF均是直角三角形,而根据等腰三角形的性质可得出∠B=∠C,由等角的余角相等即可判断④正确.
∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,BD=CD,
∴线段AD上任一点到点C、点B的距离相等,
∴①正确;
∵AD是∠BAC的平分线,
∴AD上任意一点到AB、AC的距离相等,②正确;
∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,BD=CD,
∴③正确;
∵AB=AC,
∴∠B=∠C;
∵∠BED=∠DFC=90°,
∴∠BDE=∠CDF,④正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将不等式组
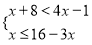 的解集在数轴上表示出来,正确的是( )
的解集在数轴上表示出来,正确的是( )A.
 B.
B. 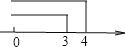
C.
 D.
D. 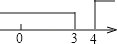
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三边长分别为a,b,c.
(1)若a,b,c满足a2+b2+c2=ab+bc+ca,试判断△ABC的形状;
(2)若a=5,b=2,且c为整数,求△ABC的周长的最大值及最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据某网站调查,2014年网民们最关注的热点话题分别有:消费、教育、环保、反腐及其他共五类.根据调查的部分相关数据,绘制的统计图表如下:

根据所给信息解答下列问题:
(1)请补全条形统计图并在图中标明相应数据;
(2)若菏泽市约有880万人口,请你估计最关注环保问题的人数约为多少万人?
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率.
-
科目: 来源: 题型:
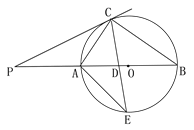
查看答案和解析>>【题目】如图,
 是
是 的直径,
的直径, 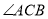 的平分线交
的平分线交 于点
于点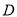 ,交
,交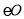 于点
于点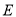 ,过点
,过点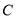 作
作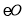 的切线
的切线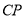 交
交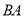 的延长线于点
的延长线于点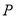 ,连接
,连接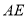 .
.
(1)求证:
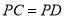 ;
;(2)若
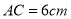 ,
,  ,求线段
,求线段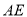 、
、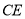 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知ABC中∠A=60°,AB=2cm,AC=6cm,点P、Q分别是边AB、AC上的动点,点P从顶点A沿AB以1cm/s的速度向点B运动,同时点Q从顶点C沿CA以3cm/s的速度向点A运动,当点P到达点B时点P、Q都停止运动.设运动的时间为t秒.

(1)当t为何值时AP=AQ;
(2)是否存在某一时刻使得△APQ是直角三角形,若存在,求出t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为4000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场的优惠条件是:每台优惠20%.
(1)设该学校所买的电脑台数是x台,选择甲商场时,所需费用为
 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为 元,请分别写出
元,请分别写出 ,
,  与x之间的关系式;
与x之间的关系式;(2)该学校如何根据所买电脑的台数选择到哪间商场购买,所需费用较少?
相关试题

