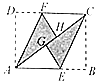
【题目】如图,在矩形纸片![]() 中,
中,![]() ,点
,点![]() 分别在
分别在![]() 上,把
上,把![]() 沿
沿![]() 翻折,
翻折,![]() 的落点是对角线
的落点是对角线![]() 上的点
上的点![]() 和
和![]() ,则四边形
,则四边形![]() 的面积是____________.
的面积是____________.
参考答案:
【答案】7.5
【解析】
直接根据矩形性质及平行四边形的判定证得四边形AECF是平行四边形,再根据勾股定理求出FC的长,最后利用平行四边形的面积公式计算即可得出结论.
解:∵翻折,
∴∠FAH=![]() ∠DAC,∠ECG=
∠DAC,∠ECG=![]() ∠BCA,
∠BCA,
∵四边形ABCD为矩形,
∴AD∥BC,AB∥CD,∠B=∠D=90°,
∴∠DAC=∠BCA,
∴∠FAH=∠ECG,
∴AF∥CE,
又∵AE∥CF,
∴四边形AECF是平行四边形,
∵在矩形纸片ABCD中,∠B=90°,AB=4,BC=3,
∴![]() ,
,
∵翻折,
∴∠FHA=∠D=90°,AH=AD=3,
同理可得,CG=3,
∴CH=AC-AH=5-3=2,
设DF=FH=x,则FC=4-x,
∵在Rt△FHC中,FC2=FH2+CH2,
∴(4-x)2=x2+22,
解得x=1.5,
∴FC=4-x=2.5,
∴四边形AECF的面积为FC·AD=2.5×3=7.5,
故答案为:7.5.
-
科目: 来源: 题型:
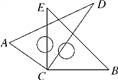
查看答案和解析>>【题目】如图,将两块直角三角尺的顶点叠放在一起.
(1)若∠DCE=35°,求∠ACB的度数;
(2)若∠ACB=140°,求∠DCE的度数;
(3)猜想∠ACB与∠DCE的关系,并说明理由.
-
科目: 来源: 题型:
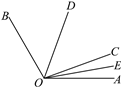
查看答案和解析>>【题目】已知∠AOC和∠BOC,OD平分∠BOC,OE平分∠AOC.
(1)请写出一对相等的角;
(2)若∠AOC在∠BOC的外部,且∠AOB=120°,如图,其他条件不变,求∠EOD的度数.从结果你能看出∠EOD与∠AOB有什么数量关系吗?
(3)若∠AOC=α,∠BOC=β(α,β都大于0°且小于180°,且α<β),其他条件不变,试求∠EOD的度数(结果用含α,β的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
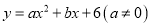 的图像交y轴于C点,交
的图像交y轴于C点,交 轴于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程
轴于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程 的两个根.
的两个根.(1)求出点A、点B的坐标及该二次函数表达式.

(2)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合),过点Q作QD∥AC交于BC点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.
(3)如图3,线段MN是直线y=x上的动线段(点M在点N左侧),且MN=
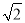 ,若M点的横坐标为n,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出n的值;若不能,请说明理由.
,若M点的横坐标为n,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出n的值;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
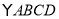 中,
中,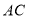 、
、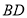 相交于点
相交于点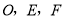 分别是
分别是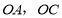 中点,连接
中点,连接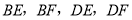 .
.(1)如图1,求证:四边形
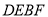 是平行四边形;
是平行四边形;(2)如图2,若
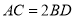 ,求证:四边形
,求证:四边形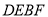 是矩形.
是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,在矩形
 中,
中,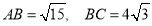 .求:①矩形
.求:①矩形 的面积
的面积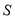 ;②对角线
;②对角线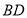 的长.
的长.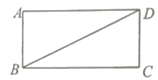
(2)如图,在菱形
 中,
中,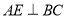 ,
,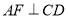 ,
, ,
,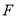 为垂足.
为垂足.①求证:
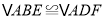 .
.②若
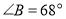 ,求
,求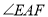 的大小.
的大小.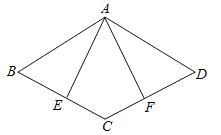
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
(1)尺规作图:过A,D,C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线.
相关试题

