搜索
【题目】下列说法中正确的是（ ）
A.有且只有一条直线与已知直线垂直；
B.从直线外一点到这条直线的垂线段，叫做这点到这条直线距离；
C.互相垂直的两条线段一定相交；
D.直线
外一点
与直线上各点连接而成的所有线段中，最短线段的长度是
，则点到直线的距离是.
参考答案：
【答案】D
【解析】
对照垂线的两条性质逐一判断．
①从直线外一点引这条直线的垂线，垂线段最短；
②过一点有且只有一条直线与已知直线垂直．
解：A、和一条直线垂直的直线有无数条，故A错误；
B、直线外一点到这条直线的垂线段的长度，叫做点到直线的距离，不是指点到直线的垂线段的本身，而是指垂线段的长度，故B错误；
C、互相垂直的两条线段不一定相交，线段有长度限制，故C错误；
D、直线l外一点A与直线l上各点连接而成的所有线段中最短线段就是垂线段，可表示点A到直线l的距离，故D正确．
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线
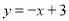与x轴、y轴分别交于点B、点C，经过B、C两点的抛物线
与x轴的另一个交点为A，顶点为P．
（1）求该抛物线的解析式；
（2）连接AC，在x轴上是否存在点Q，使以P、B、Q为顶点的三角形与△ABC相似？若存在，请求出点Q的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本题满分14分）如图，在正方形ABCD中，AB=5.点E为BC边上一点（不与点B重合），点F为CD边上一点，线段AE、BF相交于点O,其中AE=BF.
(1)求证：AE⊥BF；
(2)若OA-OB=1，求OA的长及四边形OECF的面积；
(3)连接OD,若△AOD是以AD为腰的等腰三角形，求AE的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料：
小明在学习了二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3＋2
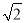＝(1＋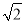
)2.善于思考的小明进行了以下探索：设a＋b
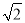＝(m＋n
)2(其中a，b，m，n均为正整数)，则有a＋b
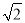＝m2＋2n2＋2mn
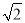.∴a＝m2＋2n2，b＝2mn.这样小明就找到了一种把部分形如a＋b
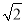的式子化为平方式的方法．请你仿照小明的方法探索并解决下列问题：
(1)当a，b，m，n均为正整数时，若a＋b
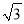＝(m＋n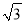
)2，用含m，n的式子分别表示a，b，得a＝__________，b＝__________；(2)利用所探索的结论，找一组正整数a，b，m，n填空：________＋________
＝(________＋________
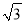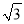)2；(3)若a＋4
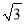＝(m＋n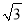
)2，且a，m，n均为正整数，求a的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知某矩形的面积为20cm 2．
(1)写出其长 y与宽 x之间的函数表达式．
(2)当矩形的长为12cm时，求宽为多少?当矩形的宽为4cm，求其长为多少?
(3)如果要求矩形的长不小于8cm，其宽至多要多少?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图图形是用同样大小的铜币摆放的四个图案，根据摆放图案的规律，则第8个图案需要铜币的个数为（ ）
A.29B.36C.37D.46
-
科目： 来源： 题型：
查看答案和解析>>【题目】小林家离工作单位的距离为3600米，他每天骑自行车上班时的速度为 v（米/分），所需时间为 t（分），
（1）则速度 v与时间 t之间有怎样的函数关系？
（2）若小林到单位用15分钟，那么他骑车的平均速度是多少？
（2）如果小林骑车的速度最快为300米/分，那他至少需要几分钟到达单位？
相关试题
