【题目】如图,E,F,G,H分别是BD,BC,AC,AD的中点,且AB=CD,下列结论:①EG⊥FH;②四边形EFGH是菱形;③HF平分∠EHG;④EG=![]() (BC﹣AD),其中正确的个数是( )
(BC﹣AD),其中正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】
根据三角形的中位线平行于第三边并且等于第三边的一半与AB=CD可得四边形EFGH是菱形;
然后根据菱形的对角线互相垂直平分,并且平分每一组对角的性质对各小题进行判断,从而找出正确的个数即可得到答案.
∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴EF=![]() CD,FG=
CD,FG=![]() AB,GH=
AB,GH=![]() CD,HE=
CD,HE=![]() AB,
AB,
∵AB=CD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形,
∴①EG⊥FH,正确;
②四边形EFGH是菱形,正确;
③HF平分∠EHG,正确;
④当AD∥BC,如图所示:E,G分别为BD,AC中点,
∴连接CD,延长EG到CD上一点N,
如下图所示:
![]()
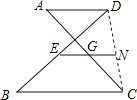
∴EN=![]() BC,GN=
BC,GN=![]() AD,
AD,
∴EG=![]() (BC-AD),只有AD∥BC时才可以成立,而本题AD与BC很显然不平行,故本小题错误;
(BC-AD),只有AD∥BC时才可以成立,而本题AD与BC很显然不平行,故本小题错误;
故①②③对.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个数值转换器,原理如下:
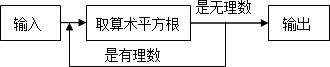
当输入的数是16时,则输出的数是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在七年级下册“证明”的一章的学习中,我们曾做过如下的实验:
画∠AOB=90°,并画∠AOB的平分线OC.
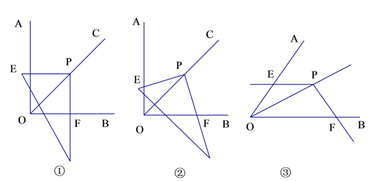
(1)把三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边分别与OA、OB相交于点E、F(如图①).度量PE、PF的长度,这两条线段相等吗?
(2)把三角尺绕点P旋转(如图②),PE与PF相等吗?请说明理由.
(3)探究:画∠AOB=50°,并画∠AOB的平分线OC,在OC上任取一点P,作∠EPF=130°.∠EPF的两边分别与OA、OB相交于E、F两点(如图③),PE与PF相等吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2
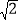 =(1+
=(1+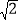 )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:设a+b=(m+n
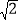 )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b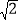 =m2+2n2+2mn
=m2+2n2+2mn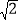 .
.∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分a+b
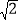 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b
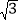 =(m+n
=(m+n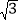 )2,用含m、n的式子分别表示a、b,得a= ,b= ;
)2,用含m、n的式子分别表示a、b,得a= ,b= ;(2)试着把7+4
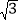 化成一个完全平方式.
化成一个完全平方式.(3)若a是216的立方根,b是16的平方根,试计算:
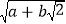 .
. -
科目: 来源: 题型:
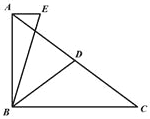
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,D为AC中点,过点A作AE∥BC,连结BE,∠EBD=∠CBD,BD=5,则BE的长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据图形填空:

(1)若直线ED,BC被直线AB所截,则∠1和__________是同位角.
(2)若直线ED,BC被直线AF所截,则∠3和__________是内错角.
(3)∠1和∠3是直线AB,AF被直线__________所截构成的__________角.
(4)∠2和∠4是直线__________,__________被直线BC所截构成的__________角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD与EF相交.
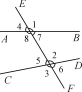
(1)图中∠1和∠2分别在直线AB,CD的同_______,并且都在直线EF的_____,具有这样位置关系的一对角叫做______;
(2)图中∠2和∠8都在直线AB,CD____,并且分别在直线EF的___,具有这样位置关系的一对角叫做_____;
(3)图中∠2和∠7都在直线AB,CD____,且都在直线EF的____,具有这样位置关系的一对角叫做______.
相关试题

