【题目】在七年级下册“证明”的一章的学习中,我们曾做过如下的实验:
画∠AOB=90°,并画∠AOB的平分线OC.
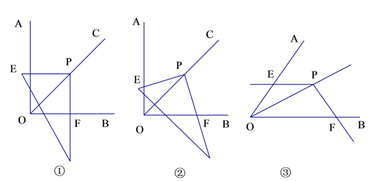
(1)把三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边分别与OA、OB相交于点E、F(如图①).度量PE、PF的长度,这两条线段相等吗?
(2)把三角尺绕点P旋转(如图②),PE与PF相等吗?请说明理由.
(3)探究:画∠AOB=50°,并画∠AOB的平分线OC,在OC上任取一点P,作∠EPF=130°.∠EPF的两边分别与OA、OB相交于E、F两点(如图③),PE与PF相等吗?请说明理由.
参考答案:
【答案】(1)PE=PF;(2)PE=PF;理由见解析;(3)PE=PF;理由见解析
【解析】试题分析:(1)由条件可知PE=PF;
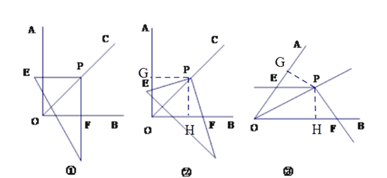
(2)过点P作PG⊥OA,PH⊥OB,垂足是G,H,利用条件证明△PEM≌△PFN即可得出结论;
(3)过点P作PG⊥OA,PH⊥OB,垂足是G,H,利用条件证明△PEM≌△PFN即可得出结论;
试题解析:(1)PE=PF;
(2)PE=PF,理由如下:
过点P作PG⊥OA,PH⊥OB,垂足是G,H,则∠PGE=∠PHF=90°,
∵OP平分∠AOB,∴PG=PH,
∵∠AOB=∠PGE=∠PHF=90°,∴∠GPH=90°,
∵∠EPF=90°,∴∠GPE=∠FPH,
∴△PEG≌△PFH(ASA),
∴PE=PF;
(3)PE=PF,理由如下:
过点P作PG⊥OA,PH⊥OB,垂足是G,H,则∠PGE=∠PHF=90°,
∵OP平分∠AOB,∴PG=PH,
∵∠AOB=50°,∴∠GPH=130°,
∵∠EPF=130°,∴∠GPE=∠FPH,
∴△PEG≌△PFH(ASA),
∴PE=PF;
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式﹣x+3≥0的正整数解有( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P1(x1,y1),点P2(x2,y2)是一次函数y=-4x+3图象上的两个点,且x1<x2,则y1与y2的大小关系是( )
A. y1>y2 B. y1>y2>0 C. y1<y2 D. y1=y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接“义务教育均衡发展”检查,我市抽查了某校七年级8个班的班额人数,抽查数据统计如下:52,49,56,54,52,51,55,54,这四组数据的众数是( )
A.52和54
B.52
C.53
D.54 -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司对350名职工进行了体重调查,如图是调查结果的统计图,请根据统计图提供的信息,回答下列问题:
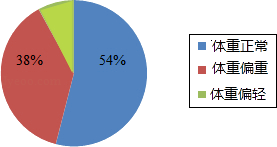
(1)体重正常的职工占的百分比是;
(2)体重正常比体重偏重的职工多占%;
(3)体重偏轻的职工有人. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把四张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形(长为a , 宽为b)的盒子底部,盒子底面未被卡片覆盖的部分用阴影表示,则这两块阴影部分小长方形周长的和为( )
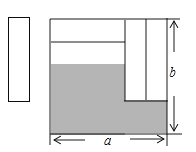
A.a+2b
B.4a
C.4b
D.2a+b -
科目: 来源: 题型:
查看答案和解析>>【题目】某快递员准备送出一批美术用纸共25500包,其中包括素描纸、手工彩色卡纸和水粉纸三种美术用纸,它们的数量比为1:2:14.该快递员准备送出的这三种美术用纸各多少包?
相关试题

