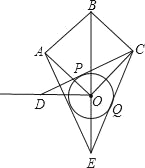
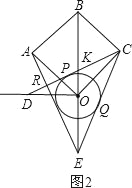
【题目】如图所示,在边长为4![]() 正方形OABC中,OB为对角线,过点O作OB的垂线.以点O为圆心,r为半径作圆,过点C做⊙O的两条切线分别交OB垂线、BO延长线于点D、E,CD、CE分别切⊙O于点P、Q,连接AE.
正方形OABC中,OB为对角线,过点O作OB的垂线.以点O为圆心,r为半径作圆,过点C做⊙O的两条切线分别交OB垂线、BO延长线于点D、E,CD、CE分别切⊙O于点P、Q,连接AE.
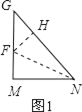
(1)请先在一个等腰直角三角形内探究tan22.5°的值;
(2)求证:
①DO=OE;
②AE=CD,且AE⊥CD.
(3)当OA=OD时:
①求∠AEC的度数;
②求r的值.
参考答案:
【答案】(1)tan22.5°=![]() ﹣1;(2)①见解析;②见解析;(3)①∠AEC的度数为45°;②r=2
﹣1;(2)①见解析;②见解析;(3)①∠AEC的度数为45°;②r=2![]()
【解析】
(1)如图1,△GMN是等腰直角三角形,过点N作NF平分∠MNG,交GM于点F,过点F作FH⊥NG于H.根据角平分线的性质可得FM=FH,利用三角函数可得GF=![]() FH,从而有GF=
FH,从而有GF=![]() FM,进而可得MN=(
FM,进而可得MN=(![]() +1)FM,在Rt△FMN中运用三角函数就可求出tan22.5°的值.
+1)FM,在Rt△FMN中运用三角函数就可求出tan22.5°的值.
(2)如图2,①易证∠DOC=∠EOC=135°,根据切线长定理可得∠PCO=∠QCO,从而可证到△DOC≌△EOC,则有OD=OE.②易证△AOE≌△COD,从而有AE=CD,∠AEO=∠CDO.由∠KDO+∠DKO=90°可得∠AEO+∠DKO=90°,即可证到AE⊥CD.
(3)连接OQ,如图3.由OC=OE得∠OEC=∠OCE,从而求出∠OEC=22.5°.在Rt△OQE中,运用三角函数可得到![]() 然后运用勾股定理就可求出r的值.
然后运用勾股定理就可求出r的值.
解:(1)如图1,△GMN是等腰直角三角形.
则有∠M=90°即GM⊥MN,MG=MN,∠MGN=∠MNG=45°.
过点N作NF平分∠MNG,交GM于点F,过点F作FH⊥NG于H.
∵NF平分∠MNG,FH⊥NG,FM⊥MN,
∴![]()
∵FH⊥NG即∠FHG=90°,∠G=45°,
∴![]()
∴GF=![]() FH.
FH.
∴GF=![]() FM.
FM.
∴MN=MG=MF+FG=MF+![]() FM=(
FM=(![]() +1)FM.
+1)FM.
在Rt△FMN中,
tan∠FNM=tan22.5°![]()
∴tan22.5°=![]() ﹣1.
﹣1.
(2)①如图2,
∵四边形OABC是正方形,
∴OA=OC,∠AOB=∠BOC=45°.
∴∠EOC=180°﹣∠BOC=135°.
∵OD⊥OB即∠DOB=90°,
∴∠DOC=∠DOB+∠BOC=135°.
∴∠DOC=∠EOC.
∵CD、CE分别与⊙O相切于P、Q,
∴∠PCO=∠QCO.
在△DOC和△EOC中,
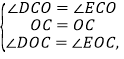
∴△DOC≌△EOC(ASA).
∴OD=OE.
②∵∠AOB=45°,
∴∠AOE=135°.
∴∠AOE=∠DOC.
在△AOE和△COD中,
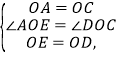
∴△AOE≌△COD(SAS).
∴AE=CD,∠AEO=∠CDO.
∵∠DOB=90°,∴∠KDO+∠DKO=90°.
∴∠AEO+∠DKO=90°.
∴∠KRE=90°.
∴AE⊥CD.
(3)①∵OA=OD,OA=OC,OD=OE,
∴OA=OD=OE=OC.
∴点A、D、E、C在以点O为圆心,OA为半径的圆上.
∴根据圆周角定理可得∠AEC=![]() ∠AOC=45°.
∠AOC=45°.
∴∠AEC的度数为45°.
②连接OQ,如图3.
∵OC=OE,∴∠OEC=∠OCE.
∵∠BOC=∠OEC+∠OCE=2∠OEC=45°,
∴∠OEC=22.5°
∵CE与⊙O相切于点Q,
∴OQ⊥EC,即∠OQE=90°.
在Rt△OQE中,
∵∠OQE=90°,
∴tan∠OEQ=tan22.5°![]()
∵OQ=r,
∴![]()
∵∠OQE=90°,
∴OQ2+QE2=OE2.
∵![]()
∴![]()
整理得![]()
解得:r=![]() .
.
∴r的值为![]() .
.
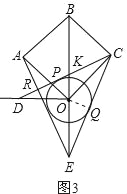
-
科目: 来源: 题型:
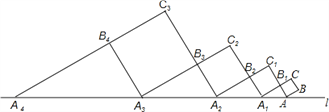
查看答案和解析>>【题目】如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3B4,…,依此规律,则A2016A2017=__.
-
科目: 来源: 题型:
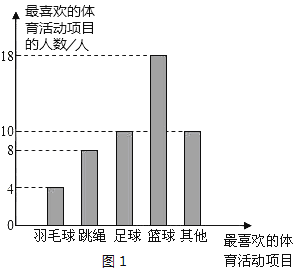
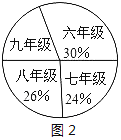
查看答案和解析>>【题目】某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据,如图1是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢足球活动的有多少人?占被调查人数的百分比是多少?
(3)若该校九年级共有400名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢篮球活动的人数约为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
-
科目: 来源: 题型:
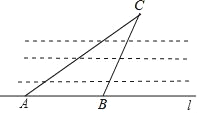
查看答案和解析>>【题目】如图,已知公路l上A、B两点之间的距离为50m,小明要测量点C与河对岸边公路l的距离,测得∠ACB=∠CAB=30°.点C到公路l的距离为( )
A. 25m B.
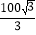 m C. 25
m C. 25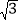 m D. (25+25
m D. (25+25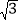 )m
)m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:
(1)∠DCF+
 ∠D=90°;(2)∠AEF+∠ECF=90°;(3)S△BEC=2S△CEF;(4)若∠B=80°,则∠AEF=50°.
∠D=90°;(2)∠AEF+∠ECF=90°;(3)S△BEC=2S△CEF;(4)若∠B=80°,则∠AEF=50°.其中一定成立的是_____(把所有正确结论的序号都填在横线上)

-
科目: 来源: 题型:
查看答案和解析>>【题目】T1、T2分别为⊙O的内接正六边形和外切正六边形.设T1的半径r,T1、T2的边长分别为a、b,T1、T2的面积分别为S1、S2.下列结论:①r:a=1:1;②r:b=
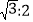 ;③a:b=1:
;③a:b=1: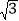 ;④S1:S2=3:4.其中正确的有_____.(填序号)
;④S1:S2=3:4.其中正确的有_____.(填序号)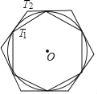
相关试题

