搜索
【题目】如图，长方形ABCD的纸片，长AD=10厘米，宽AB=8厘米，AD沿点A对折，点D正好落在BC上的点F处，AE是折痕。
（1）图中有全等的三角形吗？如果有，请直接写出来；
（2）求线段BF的长；
（3）求线段EF的长；
参考答案：
【答案】（1）有，
（2）线段BF的长为6厘米；（3）线段EF的长为5厘米.
【解析】
（1）直接利用翻折变换的性质得出△ADE≌△AFE；
（2）利用勾股定理得出BF即可；
（3）
中利用勾股定理.
解：（1）
（2）∵AD沿点A对折，点D正好落在BC上的点F处，AE是折痕,
∴AF=AD=10厘米,
在
中，AB=8厘米，AF= 10厘米，由勾股定理得：
厘米.
（3）∵AD=10厘米,BF=6厘米,
∴FC=10-6=4厘米,
在
中，设EF=
厘米,则EC=
厘米,
由勾股定理得：
,解得：
,
即EF的长为5厘米.
-
科目： 来源： 题型：
查看答案和解析>>【题目】直线y=kx+b与抛物线y=
x2交于A（x1 ， y1）、B（x2 ， y2）两点，当OA⊥OB时，直线AB恒过一个定点，该定点坐标为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】某车间计划加工360个零件，由于技术上的改进，提高了工作效率，每天比原计划多加工20%，结果提前10天完成任务，求原计划每天能加工多少个零件？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知四边形ABCD是梯形，AD∥BC，∠A＝90°，BC＝BD，CE⊥BD，垂足为E．
(1)求证：△ABD≌△ECB；
(2)若∠DBC＝50°，求∠DCE的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图1，已知△ABC，以AB、AC为边分别向外作正方形ABFD和正方形ACGE，连结BE、CD，猜想BE与CD有什么数量关系？并说明理由；
（2）请模仿正方形情景下构造全等三角形的思路，利用构造全等三角形完成下题：如图2，要测量池塘两岸相对的两点B、E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，求BE的长（结果保留根号）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，点O是等边三角形ABC内一点，∠AOB=100°，∠BOC=
, D是△ABC外一点，且△ADC ≌△BOC,连接OD.（1）求证：△COD是等边三角形；
（2）当
=150°时，请计算△AOD三内角的度数，并判断△AOD的形状；（3）探究：当
为多少度时，△AOD是等腰三角形？
-
科目： 来源： 题型：
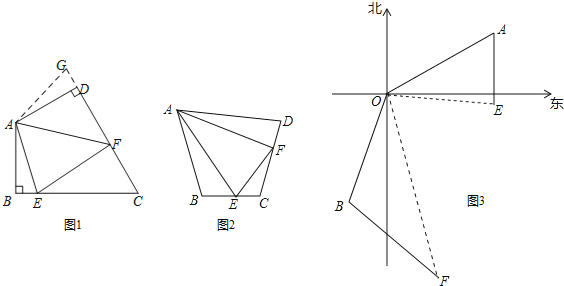
查看答案和解析>>【题目】（问题背景）如图1，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，且∠EAF＝60°，探究图中线段BE，EF，FD之间的数量关系．小明同学的方法是将△ABE绕点A逆时针旋转120°到△ADG的位置，然后再证明△AFE ≌△AFG，从而得出什么结论．
（探索延伸）如图2，若在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，E，F分别是BC，CD上的点，且∠EAF＝
∠BAD，上述结论是否仍然成立，并说明理由．（结论应用）如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏东60°的A处，舰艇乙在指挥中心南偏西20°的B处，并且两舰艇到指挥中心的距离相等．接到行动指令后，舰艇甲向正南方向以30海里/小时的速度前进，舰艇乙沿南偏东40°的方向以50海里/小时的速度前进，1小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇与指挥中心O之间夹角∠EOF＝70°，试求此时两舰艇之间的距离．
相关试题
