【题目】阅读下列材料:
我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离;即
对应的点与原点的距离;即![]() ;这个结论可以推广为
;这个结论可以推广为![]() 表示在数轴上数
表示在数轴上数![]() ,
, ![]() 对应点之间的距离.绝对值的几何意义在解题中有着广泛的应用:
对应点之间的距离.绝对值的几何意义在解题中有着广泛的应用:
例1:解方程![]() .
.
容易得出,在数轴上与原点距离为4的点对应的数为±4,即该方程的![]() ±4;
±4;
例2:解方程![]() .
.
由绝对值的几何意义可知,该方程表示求在数轴上与-1和2的距离之和为5的点对应的![]() 的值.在数轴上,-1和2的距离为3,满足方程的
的值.在数轴上,-1和2的距离为3,满足方程的![]() 对应的点在2的右边或在-1的左边.若
对应的点在2的右边或在-1的左边.若![]() 对应的
对应的
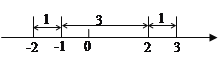
点在2的右边,如图可以看出![]() ;同理,若
;同理,若![]() 对应点在-1的左边,可得
对应点在-1的左边,可得![]() .所以原方程的解是
.所以原方程的解是![]() 或
或![]() .
.
例3:解不等式![]() .
.
在数轴上找出![]() 的解,即到1的距离为3的点对应的数为-2,4,如图,在-2的左边或在4的右边的
的解,即到1的距离为3的点对应的数为-2,4,如图,在-2的左边或在4的右边的![]() 值就满足
值就满足![]() ,所以
,所以![]() 的解为
的解为![]() 或
或![]() .
.
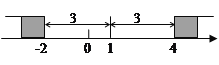
参考阅读材料,解答下列问题:
(1)方程![]() 的解为 ;
的解为 ;
(2)方程![]() 的解为 ;
的解为 ;
(3)若![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)x=2或x=-8(2)x=-2或x=2018(3)x≥5或x≤-6
【解析】试题分析:1)分类讨论:x<-3,x≥-3,可化简绝对值,根据解方程,可得答案;
(2)分类讨论:x<-1,-1≤x<2017,x≥2017,根据绝对值的意义,可化简方程,根据解方程,可得答案;
(3)![]() 表示的几何意义分情况讨论即可求解.
表示的几何意义分情况讨论即可求解.
试题解析:(1)当x<3时,原方程等价于x3=5.解得x=-8;
当x3时,原方程等价于x+3=5,解得x=2,
故答案为:x=2或x=-8;
(2)当x<1时,原方程等价于x+2017x-1=2020,解得x=2,
当1x<2017时,原方程等价于x+2017+x+1=2020,不存在x的值;
当x2017时,原方程等价于x2017+x+1=2020,解得x=2018,
综上所述:x=-2或x=2018是方程的解;
(3)∵![]() 表示的几何意义是在数轴上分别与-4和3的点的距离之和,
表示的几何意义是在数轴上分别与-4和3的点的距离之和,
而-4与3之间的距离为7,
当![]() 在-4和3时之间,
在-4和3时之间,
不存在![]() ,使
,使![]() 成立,
成立,
当![]() 在3的右边时,
在3的右边时,
如图所示,
![]()
易知当![]() 时,满足
时,满足![]() ,
,
当![]() 在-4的左边时,
在-4的左边时,
如图所示,易知当![]() 时,满足
时,满足![]() ,
,
所以![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列四个选项中,能判定四边形ABCD是平行四边形的是( )
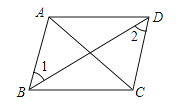
A.AB=CD,AD∥BC
B.AB∥DC,∠A=∠B
C.AB∥DC,AD=BC
D.AB∥DC,AB=DC -
科目: 来源: 题型:
查看答案和解析>>【题目】若xy>0,z<0,那么xyz0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=-1是关于x的一元二次方程x2+3x+a=0的一个根,则a的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当一个多边形的边数增加时,其外角和( )
A. 增加 B. 减少 C. 不变 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果|x﹣3|=2,那么x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解方程x2﹣4x﹣5=0时,原方程应变形为( )
A.(x+2)2=9B.(x+4)2=21C.(x﹣4)2=21D.(x﹣2)2=9
相关试题

