【题目】如图,在平面直角坐标系中,已知点A(8,1),B(0,﹣3),反比例函数y=![]() (x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(1)求k的值。
(2)求△BMN面积的最大值。
(3)若MA⊥AB,求t的值。
参考答案:
【答案】
(1)
解:把点A(8,1)代入反比例函数y=![]() (x>0)得:
(x>0)得:
k=1×8=8,y=![]() ,
,
∴k=8
(2)
解:设直线AB的解析式为:y=kx+b,
根据题意得:![]() ,
,
解得:k=![]() ,b=﹣3,
,b=﹣3,
∴直线AB的解析式为:y=![]() x﹣3;
x﹣3;
设M(t,![]() ),N(t,
),N(t,![]() t﹣3),
t﹣3),
则MN=![]() ﹣
﹣![]() t+3,
t+3,
∴△BMN的面积S=![]() (
(![]() ﹣
﹣![]() t+3)t=﹣
t+3)t=﹣![]() t2+
t2+![]() t+4=﹣
t+4=﹣![]() (t﹣3)2+
(t﹣3)2+![]() ,
,
∴△BMN的面积S是t的二次函数,
∵﹣![]() <0,
<0,
∴S有最大值,
当t=3时,△BMN的面积的最大值为![]()
(3)
解:∵MA⊥AB,
∴设直线MA的解析式为:y=﹣2x+c,
把点A(8,1)代入得:c=17,
∴直线AM的解析式为:y=﹣2x+17,
解方程组 得:
得: 或
或![]() (舍去),
(舍去),
∴M的坐标为(![]() ,16),
,16),
∴t=![]()
【解析】(1)把点A坐标代入y=![]() (x>0),即可求出k的值;
(x>0),即可求出k的值;
(2)先求出直线AB的解析式,设M(t,![]() ),N(t,
),N(t,![]() t﹣3),则MN=
t﹣3),则MN=![]() ﹣
﹣![]() t+3,由三角形的面积公式得出△BMN的面积是t的二次函数,即可得出面积的最大值;
t+3,由三角形的面积公式得出△BMN的面积是t的二次函数,即可得出面积的最大值;
(3)求出直线AM的解析式,由反比例函数解析式和直线AM的解析式组成方程组,解方程组求出M的坐标,即可得出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D.

-
科目: 来源: 题型:
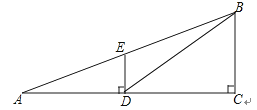
查看答案和解析>>【题目】如图,观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上,从点A处测得楼顶端B的仰角为22°,此时点E恰好在AB上,从点D处测得楼顶端B的仰角为38.5°.已知旗杆DE的高度为12米,试求楼房CB的高度.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F
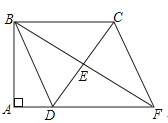
(1)求证:四边形BDFC是平行四边形。
(2)若△BCD是等腰三角形,求四边形BDFC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:⊙O上两个定点A,B和两个动点C,D,AC与BD交于点E.

(1)如图1,求证:EAEC=EBED
(2)如图2,若 , AD是⊙O的直径,求证:ADAC=2BDBC
, AD是⊙O的直径,求证:ADAC=2BDBC
(3)如图3,若AC⊥BD,点O到AD的距离为2,求BC的长 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形ABCD和正方形DEFG的边长分别为2a,2b,点A,D,G在y轴上,坐标原点O为AD的中点,抛物线y=mx2过C,F两点,连接FD并延长交抛物线于点M.

(1)若a=1,求m和b的值。
(2)求 的值。
的值。
(3)判断以FM为直径的圆与AB所在直线的位置关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A.
B.
C.
D.
相关试题

