【题目】如图,观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上,从点A处测得楼顶端B的仰角为22°,此时点E恰好在AB上,从点D处测得楼顶端B的仰角为38.5°.已知旗杆DE的高度为12米,试求楼房CB的高度.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80)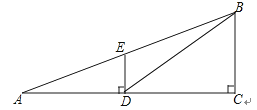
参考答案:
【答案】解:∵ED⊥AC,BC⊥AC,
∴ED∥BC,
∴△AED∽△ABC,
∴![]() =
=![]() ,
,
在Rt△AED中,DE=12米,∠A=22°,
∴tan22°=![]() ,即AD=
,即AD=![]() =30米,
=30米,
在Rt△BDC中,tan∠BDC=![]() ,即tan38.5°=
,即tan38.5°=![]() =0.8①,
=0.8①,
∵tan22°=![]() =
=![]() =0.4②,
=0.4②,
联立①②得:BC=24米.
【解析】由ED与BC都和AC垂直,得到ED与BC平行,得到三角形AED与三角形ABC相似,由相似得比例,在直角三角形AED中,利用锐角三角函数定义求出AD的长,在直角三角形BDC中,利用锐角三角函数定义求出BC的长即可.
【考点精析】本题主要考查了关于仰角俯角问题的相关知识点,需要掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:x2+2x=3;
(2)解方程组:
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 , 并补全频数分布直方图
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F
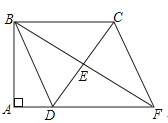
(1)求证:四边形BDFC是平行四边形。
(2)若△BCD是等腰三角形,求四边形BDFC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(8,1),B(0,﹣3),反比例函数y=
 (x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(1)求k的值。
(2)求△BMN面积的最大值。
(3)若MA⊥AB,求t的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:⊙O上两个定点A,B和两个动点C,D,AC与BD交于点E.

(1)如图1,求证:EAEC=EBED
(2)如图2,若 , AD是⊙O的直径,求证:ADAC=2BDBC
, AD是⊙O的直径,求证:ADAC=2BDBC
(3)如图3,若AC⊥BD,点O到AD的距离为2,求BC的长
相关试题

