【题目】如图,在平面直角坐标系中,正方形ABCD和正方形DEFG的边长分别为2a,2b,点A,D,G在y轴上,坐标原点O为AD的中点,抛物线y=mx2过C,F两点,连接FD并延长交抛物线于点M.
(1)若a=1,求m和b的值。
(2)求![]() 的值。
的值。
(3)判断以FM为直径的圆与AB所在直线的位置关系,并说明理由.
参考答案:
【答案】
(1)
解:(1)∵a=1,
∴正方形ABCD的边长为2,
∵坐标原点O为AD的中点,
∴C(2,1).
∵抛物线y=mx2过C点,
∴1=4m,解得m=![]() ,
,
∴抛物线解析式为y=![]() x2,
x2,
将F(2b,2b+1)代入y=![]() x2,
x2,
得2b+1=![]() ×(2b)2,b=1±
×(2b)2,b=1±![]() (负值舍去).
(负值舍去).
故m=![]() ,b=1+
,b=1+![]()
(2)
解:∵正方形ABCD的边长为2a,坐标原点O为AD的中点,
∴C(2a,a).
∵抛物线y=mx2过C点,
∴a=m4a2,解得m=![]() ,
,
∴抛物线解析式为y=![]() x2,
x2,
将F(2b,2b+a)代入y=![]() x2,
x2,
得2b+a=![]() ×(2b)2,
×(2b)2,
整理得b2﹣2ab﹣a2=0,
解得b=(1±![]() )a(负值舍去),
)a(负值舍去),
∴![]() =1+
=1+![]()
(3)
解:以FM为直径的圆与AB所在直线相切.理由如下:
∵D(0,a),
∴可设直线FD的解析式为y=kx+a,
∵F(2b,2b+a),
∴2b+a=k2b+a,解得k=1,
∴直线FD的解析式为y=x+a.
将y=x+a代入y=![]() x2,
x2,
得x+a=![]() x2,解得x=2a±2
x2,解得x=2a±2![]() a(正值舍去),
a(正值舍去),
∴M点坐标为(2a﹣2![]() a,3a﹣2
a,3a﹣2![]() a).
a).
∵F(2b,2b+a),b=(1+![]() )a,
)a,
∴F(2a+2![]() a,3a+2
a,3a+2![]() a),
a),
∴以FM为直径的圆的圆心O′的坐标为(2a,3a),
∴O′到直线AB(y=﹣a)的距离d=3a﹣(﹣a)=4a,
∵以FM为直径的圆的半径r=O′F=![]() =4a,
=4a,
∴d=r,
∴以FM为直径的圆与AB所在直线相切.
【解析】(1)由a=1,根据正方形的性质及已知条件得出C(2,1).将C点坐标代入y=mx2 , 求出m=![]() ,则抛物线解析式为y=
,则抛物线解析式为y=![]() x2 , 再将F(2b,2b+1)代入y=
x2 , 再将F(2b,2b+1)代入y=![]() x2 , 即可求出b的值;
x2 , 即可求出b的值;
(2)由正方形ABCD的边长为2a,坐标原点O为AD的中点,得出C(2a,a).将C点坐标代入y=mx2 , 求出m=![]() ,则抛物线解析式为y=
,则抛物线解析式为y=![]() x2 , 再将F(2b,2b+a)代入y=
x2 , 再将F(2b,2b+a)代入y=![]() x2 , 整理得出方程b2﹣2ab﹣a2=0,把a看作常数,利用求根公式得出b=(1±
x2 , 整理得出方程b2﹣2ab﹣a2=0,把a看作常数,利用求根公式得出b=(1±![]() )a(负值舍去),那么
)a(负值舍去),那么![]() =1+
=1+![]() ;
;
(3)先利用待定系数法求出直线FD的解析式为y=x+a.再求出M点坐标为(2a﹣2![]() a,3a﹣2
a,3a﹣2![]() a).又F(2a+2
a).又F(2a+2![]() a,3a+2
a,3a+2![]() a),利用中点坐标公式得到以FM为直径的圆的圆心O′的坐标为(2a,3a),再求出O′到直线AB(y=﹣a)的距离d的值,以FM为直径的圆的半径r的值,由d=r,根据直线与圆的位置关系可得以FM为直径的圆与AB所在直线相切.
a),利用中点坐标公式得到以FM为直径的圆的圆心O′的坐标为(2a,3a),再求出O′到直线AB(y=﹣a)的距离d的值,以FM为直径的圆的半径r的值,由d=r,根据直线与圆的位置关系可得以FM为直径的圆与AB所在直线相切.
此题考查了根据点的坐标和解析式求得参数,利用球根公式,待定系数法和中点坐标 公式以及点到直线距离解答相关问题。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F
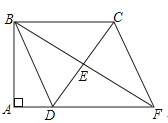
(1)求证:四边形BDFC是平行四边形。
(2)若△BCD是等腰三角形,求四边形BDFC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(8,1),B(0,﹣3),反比例函数y=
 (x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(1)求k的值。
(2)求△BMN面积的最大值。
(3)若MA⊥AB,求t的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:⊙O上两个定点A,B和两个动点C,D,AC与BD交于点E.

(1)如图1,求证:EAEC=EBED
(2)如图2,若 , AD是⊙O的直径,求证:ADAC=2BDBC
, AD是⊙O的直径,求证:ADAC=2BDBC
(3)如图3,若AC⊥BD,点O到AD的距离为2,求BC的长 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AD、BE分别是△ABC的中线和角平分线,AD⊥BE,AD=BE=6,则AC的长等于 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场在“五一”期间举行促销活动,根据顾客按商品标价一次性购物总额,规定相应的优惠方法:①如果不超过500元,则不予优惠;②如果超过500元,但不超过800元,则按购物总额给予8折优惠;③如果超过800元,则其中800元给予8折优惠,超过800元的部分给予6折优惠.促销期间,小红和她母亲分别看中一件商品,若各自单独付款,则应分别付款480元和520元;若合并付款,则她们总共只需付款 元.
相关试题

