【题目】读图并回答下列问题:
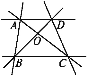
(1)过点A的直线有哪几条?
(2)以O为端点的射线有哪几条?
(3)写出图中所有的线段.
(4)∠ABC是哪两个角的和?
(5)比较线段AB,OB的长短.
参考答案:
【答案】(1)有三条:直线AB、直线AC、直线AD;(2)有四条:射线OA、射线OB、射线OC、射线OD;(3)线段AB,BC,CD,AD,OA,OC,OB,OD,AC,BD;(4)∠ABO与∠CBO;(5) AB>OB.
【解析】
(1)图中过点A的直线有三条;
(2)根据数射线的方法数出即可;
(3)根据数线段的方法数出即可;
(4)由图即可得出;
(5)用度量法或圆规即可比较.
(1)过点A的直线有三条:直线AB、直线AC、直线AD;
(2)以O为端点的射线有四条:射线OA、射线OB、射线OC、射线OD;
(3)图中的线段分别为线段AB,BC,CD,AD,OA,OC,OB,OD,AC,BD;
(4)∠ABO与∠CBO;
(5)利用刻度尺或圆规可得AB>OB.
-
科目: 来源: 题型:
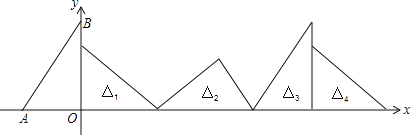
查看答案和解析>>【题目】如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2016的直角顶点的坐标为 ( )
A. 8065 B. 8064 C. 8063 D. 8062
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具店进了一排黑白塑料球,共5箱,每箱的规格、数量都相同,其中每箱中装有黑白两种颜色的塑料球共3000个,为了估计每箱中两种颜色球的个数,随机抽查了一箱,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,发现摸到黑球的概率在0.8附近波动,则此可以估计这批塑料球中黑球的总个数,请将黑球总个数用科学记数法表示约为个.
-
科目: 来源: 题型:
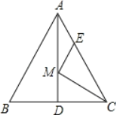
查看答案和解析>>【题目】如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=2,EM+CM的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
65
124
178
302
481
599
1803
摸到白球的频率=
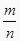
0.65
0.62
0.593
0.604
0.601
0.599
0.601
(1)请估计:当n很大时,摸到白球的频率将会接近多少?(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)是多少?
(3)试估算盒子里黑、白两种颜色的球各有多少只? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB=4,点O是线段AB上的点,点C,D是线段OA,OB的中点,小明很轻松地求得CD=2.

(1)小明在反思过程中突发奇想:若点O运动到线段AB的延长线上,则原有的结论“CD=2”是否仍然成立呢?请帮小明画出图形分析,并说明理由.
(2)当点O运动到直线AB外时,结论“CD=2”是否还成立?请利用刻度尺验证你的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内部,∠BOE=
 ∠EOC,∠DOE=70°,求∠EOC的度数.
∠EOC,∠DOE=70°,求∠EOC的度数.
相关试题

