【题目】某玩具店进了一排黑白塑料球,共5箱,每箱的规格、数量都相同,其中每箱中装有黑白两种颜色的塑料球共3000个,为了估计每箱中两种颜色球的个数,随机抽查了一箱,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,发现摸到黑球的概率在0.8附近波动,则此可以估计这批塑料球中黑球的总个数,请将黑球总个数用科学记数法表示约为个.
参考答案:
【答案】1.2×104
【解析】设黑球的个数为x,
∵黑球的频率在0.8附近波动,
∴摸出黑球的概率为0.8,即 ![]() =0.8,
=0.8,
解得x=2400.
所以可以估计黑球的个数为2400×5=12000=1.2×104个,
所以答案是:1.2×104 .
【考点精析】本题主要考查了用频率估计概率的相关知识点,需要掌握在同样条件下,做大量的重复试验,利用一个随机事件发生的频率逐渐稳定到某个常数,可以估计这个事件发生的概率才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时),图中折线OABC、线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图像线段AB表示甲出发不足2小时因故停车检修),请根据图像所提供的信息,解决如下问题:
(1)求乙车所行路程y与时间x的函数关系式;
(2)求两车在途中第二次相遇时,它们距出发地的路程;
(3)乙车出发多长时间,两车在途中第一次相遇?(写出解题过程)

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( ).
(A)周长相等的锐角三角形都全等; (B) 周长相等的直角三角形都全等;
(C)周长相等的钝角三角形都全等; (D) 周长相等的等腰直角三角形都全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2016的直角顶点的坐标为 ( )
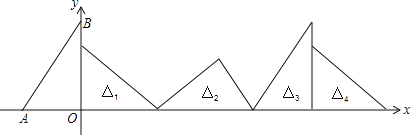
A. 8065 B. 8064 C. 8063 D. 8062
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=2,EM+CM的最小值为 .
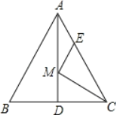
-
科目: 来源: 题型:
查看答案和解析>>【题目】读图并回答下列问题:
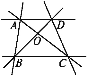
(1)过点A的直线有哪几条?
(2)以O为端点的射线有哪几条?
(3)写出图中所有的线段.
(4)∠ABC是哪两个角的和?
(5)比较线段AB,OB的长短.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
65
124
178
302
481
599
1803
摸到白球的频率=
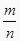
0.65
0.62
0.593
0.604
0.601
0.599
0.601
(1)请估计:当n很大时,摸到白球的频率将会接近多少?(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)是多少?
(3)试估算盒子里黑、白两种颜色的球各有多少只?
相关试题

