【题目】如图,线段AB=4,点O是线段AB上的点,点C,D是线段OA,OB的中点,小明很轻松地求得CD=2.
![]()
(1)小明在反思过程中突发奇想:若点O运动到线段AB的延长线上,则原有的结论“CD=2”是否仍然成立呢?请帮小明画出图形分析,并说明理由.
(2)当点O运动到直线AB外时,结论“CD=2”是否还成立?请利用刻度尺验证你的猜想.
参考答案:
【答案】(1)成立.理由见解析;(2)成立,理由见解析.
【解析】
(1)先画出几何图,再根据线段中点定义得到CO=![]() OA,DO=
OA,DO=![]() OB,于是有CD=CO-DO=
OB,于是有CD=CO-DO=![]() AB=2;
AB=2;
(2)先画出几何图,然后进行测量可得CD=2.
(1)成立.理由如下:如图所示,
![]()
CD=OC-OD=![]() (OA-OB)=
(OA-OB)=![]() AB=
AB=![]() ×4=2;
×4=2;
(2)CD=3仍然成立.
如图2,可测出CD=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点,若AE=2,EM+CM的最小值为 .
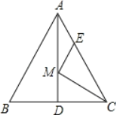
-
科目: 来源: 题型:
查看答案和解析>>【题目】读图并回答下列问题:
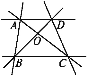
(1)过点A的直线有哪几条?
(2)以O为端点的射线有哪几条?
(3)写出图中所有的线段.
(4)∠ABC是哪两个角的和?
(5)比较线段AB,OB的长短.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
65
124
178
302
481
599
1803
摸到白球的频率=
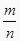
0.65
0.62
0.593
0.604
0.601
0.599
0.601
(1)请估计:当n很大时,摸到白球的频率将会接近多少?(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)是多少?
(3)试估算盒子里黑、白两种颜色的球各有多少只? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内部,∠BOE=
 ∠EOC,∠DOE=70°,求∠EOC的度数.
∠EOC,∠DOE=70°,求∠EOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是2015年12月月历.
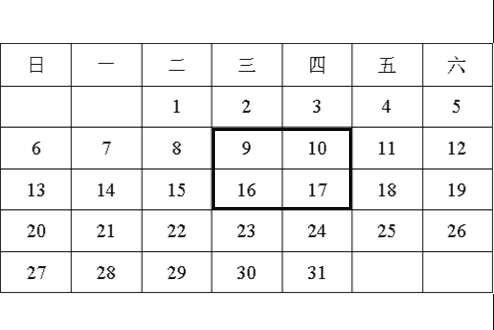
(1)如图,用一正方形框在表中任意框往4个数,记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是 , , .
(2)在表中框住四个数之和最小记为a1,和最大记为a2,则a1+a2= .
(3)当(1)中被框住的4个数之和等于76时,x的值为多少?
(4)在(1)中能否框住这样的4个数,它们的和等于92?若能,则求出x的值;若不能,则说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料: 在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:

小敏的作法如下:
如图,
①链接op,做线段op的垂直平分线MN,交OP于点C
②以点C为圆心,CO的长为半径作圆,交⊙O于A、B两点
③作直线PA、PB所以直线PA,PB就是所求的切线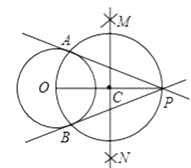
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是;由此可证明直线PA,PB都是⊙O的切线,其依据是
相关试题

