【题目】如图,在△ABC中,AB=8cm,BC=16cm,点P从点A出发沿AB边想向点B以2cm/s的速度移动,点Q从点B出发沿BC边向点C以4cm/s的速度移动,如果P、Q同时出发,经过几秒后△PBQ和△ABC相似? 
参考答案:
【答案】解:设经过x秒后△PBQ和△ABC相似.
则AP=2x cm,BQ=4x cm,
∵AB=8cm,BC=16cm,
∴BP=(8﹣2x)cm,
①BP与BC边是对应边,则 ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得x=0.8,
②BP与AB边是对应边,则 ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得x=2.
综上所述,经过0.8秒或2秒后△PBQ和△ABC相似
【解析】设经过x秒两三角形相似,分别表示出BP、BQ的长度,再分①BP与BC边是对应边,②BP与AB边是对应边两种情况,根据相似三角形对应边成比例列出比例式求解即可.
【考点精析】本题主要考查了相似三角形的性质的相关知识点,需要掌握对应角相等,对应边成比例的两个三角形叫做相似三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为 .

-
科目: 来源: 题型:
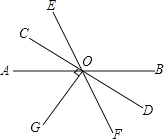
查看答案和解析>>【题目】如图,直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=32°.
(1)求∠AOG的度数;
(2)如果OC是∠AOE的平分线,那么OG是∠AOF的平分线吗?请说明理由.
-
科目: 来源: 题型:
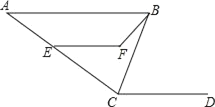
查看答案和解析>>【题目】如图,AB∥CD,CB平分∠ACD,∠ACD=140°,∠CBF=20°,∠EFB=130°.求∠CEF的度数.
-
科目: 来源: 题型:
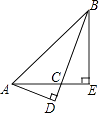
查看答案和解析>>【题目】如图所示,AD,BE是钝角△ABC的边BC,AC上的高,求证:
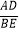 =
= 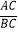 .
. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.

若某户居民
 月份用水
月份用水 ,则应收水费:
,则应收水费: 元.
元.(1)若该户居民
 月份用水
月份用水 ,则应收水费______元;
,则应收水费______元;(2)若该户居民
 、
、 月份共用水
月份共用水 (
( 月份用水量超过
月份用水量超过 月份),共交水费
月份),共交水费 元,则该户居民
元,则该户居民 ,
, 月份各用水多少立方米?
月份各用水多少立方米? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2﹣4a(a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.
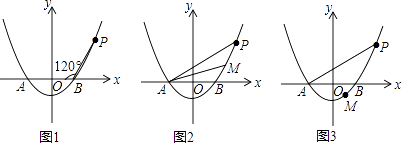
(1)求抛物线的解析式.
(2)设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.
①当点M在曲线PB之间(含端点)移动时,是否存在点M使△APM的面积为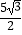 ?若存在,求点M的坐标;若不存在,请说明理由.
?若存在,求点M的坐标;若不存在,请说明理由.
②当点M在曲线BA之间(含端点)移动时,求|m|+|n|的最大值及取得最大值时点M的坐标.
相关试题

