【题目】Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,以点C为圆心5cm为半径的圆与直线AB的位置关系是( )
A.相交
B.相切
C.相离
D.无法确定
参考答案:
【答案】A
【解析】解:过C点作CD⊥AB,垂足为D, ∵∠C=90°,BC=6,AC=8,
由勾股定理,得AB= ![]() =10,
=10,
根据三角形计算面积的方法可知,BC×AC=AB×CD,
∴CD= ![]() =4.8<5,
=4.8<5,
∴⊙C与直线AB相交.
故选A.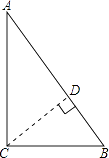
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对直线与圆的三种位置关系的理解,了解直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一种单价为40元的书包,如果以单价50元出售,那么每月可售出30个,根据销售经验,售价每提高5元,销售量相应减少1个.
(1)请写出销售单价提高x元与总的销售利润y元之间的函数关系式;
(2)如果你是经理,为使每月的销售利润最大,那么你确定这种书包的单价为多少元?此时,最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AM、BN分别与⊙O相切于点A、B,CD交AM、BN于点D、C,DO平分∠ADC.

(1)求证:CD是⊙O的切线;
(2)设AD=4,AB=x (x>0),BC=y (y>0).求y关于x的函数解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线与x轴只有一个交点A(﹣2,0),与y轴交于点B(0,4).

(1)求抛物线对应的函数解析式;
(2)过点B作平行于x轴的直线交抛物线与点C.
①若点M在抛物线的AB段(不含A、B两点)上,求四边形BMAC面积最大时,点M的坐标;
②在平面直角坐标系内是否存在点P,使以P、A、B、C为顶点的四边形是平行四边形,若存在直接写出所有满足条件的点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+b与反比例函数y=
 在同一平面直角坐标系中的图象可能是( )
在同一平面直角坐标系中的图象可能是( )
A.
B.
C.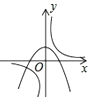
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图(虚线部分为对称轴),给出以下5个结论:①x≤1时,y随x的增大而增大;②abc>0;③b<a+c;④4a+2b+c>0;⑤3a﹣b<0,其中正确的结论有(填上所有正确结论的序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,
 =
=  ,且AB=5,BD=4,求弦DE的长.
,且AB=5,BD=4,求弦DE的长. 
相关试题

