【题目】二次函数y=ax2+b与反比例函数y= 在同一平面直角坐标系中的图象可能是（ ）
A.
B.
C.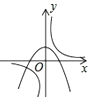
D.

参考答案：

【答案】B
【解析】解：A、根据抛物线开口向上，与y轴交于正半轴可得a＞0，b＞0，即ab＞0，所以双曲线在第一、三象限，故A选项错误； B、根据抛物线开口向上，与y轴交于正半轴可得a＞0，b＞0，即ab＞0，所以双曲线在第一、三象限，故B选项正确；
C、根据抛物线开口向下，与y轴交于正半轴可得a＜0，b＞0，即ab＜0，所以双曲线在第二、四象限，故C选项错误；
D、根据抛物线开口向上，与y轴交于负半轴可得a＞0，b＜0，即ab＜0，所以双曲线在第二、四象限，故D选项错误．
故选：B．
【考点精析】掌握反比例函数的图象和反比例函数的性质是解答本题的根本，需要知道反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点；性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大．

关闭