【题目】如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论:(1)BP=CM;(2)△ABQ≌△CAP;(3)∠CMQ的度数始终等于60°;(4)当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形.其中正确的结论有( )
秒时,△PBQ为直角三角形.其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
参考答案:
【答案】 C
【解析】
试题分析:易证△ABQ≌△CAP,可得∠AQB=∠CPA,即可求得∠AMP=∠B=60°,易证∠CQM≠60°,可得CQ≠CM,根据t的值易求BP,BQ的长,即可求得PQ的长,即可解题. ∵△ABC是等边三角形,
∴AB=BC=AC,∠BAC=∠B=∠ACB=60°, 根据题意得:AP=BQ, 在△ABQ和△CAP中,
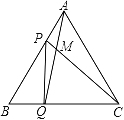
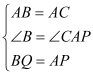 , ∴△ABQ≌△CAP(SAS),(2)正确; ∴∠AQB=∠CPA,
, ∴△ABQ≌△CAP(SAS),(2)正确; ∴∠AQB=∠CPA,
∵∠BAQ+∠APC+∠AMP=180°,∠BAQ+∠B+∠AQB=180°, ∴∠AMP=∠B=60°,
∴∠QMC=60°,(3)正确; ∵∠QMC=60°,∠QCM≠60°, ∴∠CQM≠60°, ∴CQ≠CM,
∵BP=CQ, ∴CM≠BP,(1)错误; 当t=![]() 时,BQ=
时,BQ=![]() ,BP=4﹣
,BP=4﹣![]() =
=![]() ,
,
∵PQ2=BP2+BQ2﹣2BPBQcos60°, ∴PQ=![]() , ∴△PBQ为直角三角形,
, ∴△PBQ为直角三角形,
同理t=![]() 时,△PBQ为直角三角形仍然成立,(4)正确;
时,△PBQ为直角三角形仍然成立,(4)正确;
-
科目: 来源: 题型:
查看答案和解析>>【题目】袋中装有除颜色外完全相同的2个红球和1个绿球.
(1)现从袋中摸出1个球后放回,混合均匀后再摸出1个球.请用画树状图或列表的方法,求第一次摸到绿球,第二次摸到红球的概率;
(2)先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是多少?请直接写出结果.
-
科目: 来源: 题型:
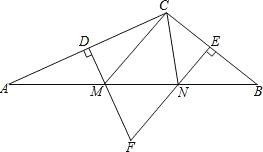
查看答案和解析>>【题目】如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若△CMN的周长为15cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,⊙O的半径为3,
 的长为π.
的长为π.
(1)直线CD与⊙O相切吗?说明理由。
(2)求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解2013年昆明市九年级学生学业水平考试的数学成绩,从中随机抽取1 000名学生的数学成绩,下列说法正确的是( )
A. 2013年昆明市九年级学生是总体 B. 每一名九年级学生是个体
C. 1 000名九年级学生是总体的一个样本 D. 样本容量是1 000
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆的面积公式S=πR2中,S与R之间的关系是( )
A. S是R的正比例函数 B. S是R的一次函数
C. S是R的二次函数 D. 以上答案都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P的坐标为(﹣1,2),则点P位于( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
相关试题

