【题目】已知函数 ![]() 是关于x的二次函数,求:
是关于x的二次函数,求:
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,当x为何值时,y随x的增大而增大;
(3)m为何值时,抛物线有最大值?最大值是多少?当x为何值时,y随x的增大而减小?
参考答案:
【答案】
(1)
解:由题意,有 ![]() 且
且 ![]() ,解之得
,解之得 ![]() 或
或 ![]() .
.
(2)
解:当 ![]() 时,二次函数有最低点,此时
时,二次函数有最低点,此时 ![]() ,最低点为(0,0),且当
,最低点为(0,0),且当 ![]() 时,y随x的增大而增大.
时,y随x的增大而增大.
(3)
解:当 ![]() 时,抛物线有最大值,最大值为0,且当
时,抛物线有最大值,最大值为0,且当 ![]() 时,y随x的增大而减小.
时,y随x的增大而减小.
【解析】二次函数 ![]() 当
当 ![]() 取正负值时,抛物线开口方向改变,增减性改变。
取正负值时,抛物线开口方向改变,增减性改变。
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用等式的性质解下列方程.
(1)y+3=2; (2)-
 y-2=3; (3)9x=8x-6; (4)8m=4m+1。
y-2=3; (3)9x=8x-6; (4)8m=4m+1。 -
科目: 来源: 题型:
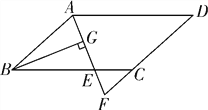
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=6,AD=10,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,AG=2.5,则△CEF的周长为
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地电话拨号上网有两种收费方式,用户可以任选其一:(A)计时制,0.05元∕分;(B)包月制,50元∕分(限一部个人住宅电话上网);此外,每种上网方式都附加通信费0.02元∕分。
(1)某用户某月上网时间为x分钟,则该用户在A、B两种收费方式下应支付费用各多少元?
(2)如果一个月内上网200分钟和300分钟,按两种收费方式各需交费多少元?
(3)是否存在某一时间,会出现两种收费方式一样的情况吗?求出这时的上网时间?
(4)如果某人一个月上网20小时,那么应选用哪一种方式较为合算?如果小明的妈妈准备办理这种业务,你能告诉她如何选择更加合算吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,∠ADC的平分线交AB于点E,∠ABC的平分线交CD于点F,求证:四边形EBFD是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D,E分别是AC,AB上的两点,且
 =
= 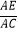 =
=  ,若△ADE的面积为1cm2 , 则四边形EBCD的面积为( )cm2 .
,若△ADE的面积为1cm2 , 则四边形EBCD的面积为( )cm2 . 
A.2
B.3
C.4
D.5 -
科目: 来源: 题型:
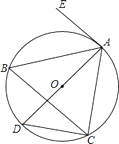
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是( )
A.80°
B.70°
C.60°
D.50°
相关试题

