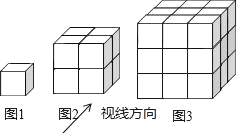
【题目】如图所示,每个小立方体的棱长为1,按如图所示的视线方向看,图1中共有1个1立方体,其中1个看得见,0个看不见;图2中共有8个立方体,其中7个看得见,1个看不见;图3中共有27个小立方体,其中19个看得见,8个看不见;…,则第11个图形中,其中看得见的小立方体个数是( )
A. 271 B. 272 C. 331 D. 332
参考答案:
【答案】C
【解析】
根据图①中,共有1个小立方体,其中1个看得见,0=(1-1)3个看不见,
图②中,共有8个小立方体,其中7个看得见,1=(2-1)3个看不见,
图③中,共有27个小立方体,其中19个看得见,8=(3-1)3个看不见,…,
归纳出变化规律:
第n个图中,一切看不见的棱长为1的小立方体的个数为(n-1)3,
看见立方体的个数为n3-(n-1)3,将第11个代入即可求解.
图①中,共有1个小立方体,其中1个看得见,0=(1-1)3个看不见,
图②中,共有8个小立方体,其中7个看得见,1=(2-1)3个看不见,
图③中,共有27个小立方体,其中19个看得见,8=(3-1)3个看不见,…,
第n个图中,一切看不见的棱长为1的小立方体的个数为(n-1)3,
看见立方体的个数为n3-(n-1)3,
所以则第11个图形中,其中看得见的小立方体有113-103=331个,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
思路:(1) 作AD⊥BC于D,设BD = x,用含x的代数式表示CD;(2)根据勾股定理,利用AD作为“桥梁”,建立方程模型,求出x;(3)利用勾股定理求出AD的长,再计算三角形面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知多项式(2x2+ax﹣y+6)﹣(2bx2﹣3x+5y﹣1).
(1)若多项式的值与字母x的取值无关,求a、b的值.
(2)在(1)的条件下,先化简多项式3(a2﹣ab+b2)﹣(3a2+ab+b2),再求它的值.
(3)在(1)的条件下,求(b+a2)+(2b+
 a2)+(3b+
a2)+(3b+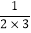 a2)+…+(9b+
a2)+…+(9b+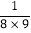 a2)的值.
a2)的值. -
科目: 来源: 题型:
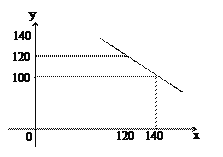
查看答案和解析>>【题目】某商店试销一种成本单价为100元/件的运动服,规定试销时的销售单价不低于成本单价,又不高于180元/件,经市场调查,发现销售量y(件)与销售单价x(元)之间的关系满足一次函数y=kx+b(k≠0),其图象如图。
(1)根据图象,求一次函数的解析式;
(2)当销售单价x在什么范围内取值时,销售量y不低于80件。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:(﹣1)2018﹣8÷(﹣2)3+4×(﹣
 )3;
)3;(2)先化简,再求值:3(a2b﹣2ab2)﹣(3a2b﹣2ab2),其中|a﹣1|+(b+
 )2=0.
)2=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C,D为线段AB上的两点,M,N分别是线段AC,BD的中点.
(1)如果CD=5cm,MN=8cm,求AB的长;
(2)如果AB=a,MN=b,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,AD与⊙O相切于点B,D,C为⊙O上一点,且∠BCD=140°,则∠A的度数是( )

A.70°
B.105°
C.100°
D.110°
相关试题

