【题目】如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
(1)求此抛物线的解析式;
(2)在直线AC上有一动点E,当点E在某个位置时,使△BDE的周长最小,求此时E点坐标;
(3)当动点E在直线AC与抛物线围成的封闭线A→C→B→D→A上运动时,是否存在使△BDE为直角三角形的情况,若存在,请直接写出符合要求的E点的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,
∴ ![]() ,
,
∴ ![]() ,
,
∴抛物线解析式为y=x2﹣3x﹣4
(2)
解:如图1,

作点B关于直线AC的对称点F,连接DF交AC于点E,
由(1)得,抛物线解析式为y=x2﹣3x﹣4①,
∴D(0,﹣4),
∵点C是直线y=﹣x+4②与抛物线的交点,
∴联立①②解得, ![]() (舍)或
(舍)或 ![]() ,
,
∴C(﹣2,6),
∵A(4,0),
∴直线AC解析式为y=﹣x+4,
∵直线BF⊥AC,且B(﹣1,0),
∴直线BF解析式为y=x+1,
设点F(m,m+1),
∴G( ![]() ,
, ![]() ),
),
∵点G在直线AC上,
∴﹣ ![]() ,
,
∴m=4,
∴F(4,5),
∵D(0,﹣4),
∴直线DF解析式为y= ![]() x﹣4,
x﹣4,
∵直线AC解析式为y=﹣x+4,
∴直线DF和直线AC的交点E( ![]() ,
, ![]() )
)
(3)
解:∵BD= ![]() ,
,
由(2)有,点B到线段AC的距离为BG= ![]() BF=
BF= ![]() ×5
×5 ![]() =
= ![]() >BD,
>BD,
∴∠BED不可能是直角,
∵B(﹣1,0),D(0,﹣4),
∴直线BD解析式为y=﹣4x+4,
∵△BDE为直角三角形,
∴①∠BDE=90°,
∴BE⊥BD交AC于B,
∴直线BE解析式为y= ![]() x+
x+ ![]() ,
,
∵点E在直线AC:y=﹣x+4的图象上,
∴E(3,1),
②∠BDE=90°,
∴BE⊥BD交AC于D,
∴直线BE的解析式为y= ![]() x﹣4,
x﹣4,
∵点E在抛物线y=x2﹣3x﹣4上,
∴直线BE与抛物线的交点为(0,﹣4)和( ![]() ,﹣
,﹣ ![]() ),
),
∴E( ![]() ,﹣
,﹣ ![]() ),
),
即:满足条件的点E的坐标为E(3,1)或( ![]() ,﹣
,﹣ ![]() )
)
【解析】(1)利用待定系数法求出抛物线解析式;(2)先判断出周长最小时BE⊥AC,即作点B关于直线AC的对称点F,连接DF,交AC于点E,联立方程组即可;(3)三角形BDE是直角三角形时,由于BD>BG,因此只有∠DBE=90°或∠BDE=90°,两种情况,利用直线垂直求出点E坐标.此题是二次函数综合题,主要考查了待定系数法,极值,对称性,直角三角形的性质,解本题的关键是求函数图象的交点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角坐标系xoy中,直线l:y=kx+b交x轴,y轴于点E,F,点B的坐标是(2,2),过点B分别作x轴、y轴的垂线,垂足为A、C,点D是线段CO上的动点,以BD为对称轴,作与△BCD或轴对称的△BC′D.

(1)当∠CBD=15°时,求点C′的坐标.
(2)当图1中的直线l经过点A,且k=﹣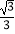 时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
(3)当图1中的直线l经过点D,C′时(如图3),以DE为对称轴,作于△DOE或轴对称的△DO′E,连结O′C,O′O,问是否存在点D,使得△DO′E与△CO′O相似?若存在,求出k、b的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时: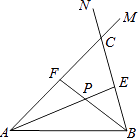
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;
(2)设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32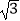 ,求AQ的长.
,求AQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且速度都为1cm/s,连接AQ、CP交于点M,下面四个结论:①BP=CM;②△ABQ≌△CAP;③∠CMQ的度数不变,始终等于60°;④当第
 秒或第
秒或第 秒时,△PBQ为直角三角形,正确的有几个 ( )
秒时,△PBQ为直角三角形,正确的有几个 ( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AO
 OM,OA=8,点B为射线OM上的一个动点,分别以OB、AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度是 ( )
OM,OA=8,点B为射线OM上的一个动点,分别以OB、AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度是 ( )
A. 3.6 B. 4 C. 4.8 D. PB的长度随B点的运动而变化
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为等腰直角三角形,D为斜边AB上任意一点,(不与点A、B重合),连接CD,作EC⊥DC,且EC=DC,连接AE,则∠EAC为_______________度.
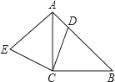
-
科目: 来源: 题型:
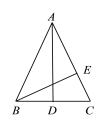
查看答案和解析>>【题目】在三角形ABC中,AB=AC,D是底边上的中点,BE垂直AC于点E,①∠ABC=∠ACB;②AD⊥BC;③∠BAD=∠CBE;④AB=2BD,其中正确的有___________.
相关试题

