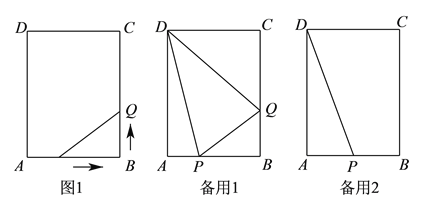
【题目】如图![]() ,在长方形
,在长方形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 从点
从点![]() 开始以
开始以![]() 的速度沿
的速度沿![]() 边向点
边向点![]() 运动,点
运动,点![]() 从点
从点![]() 以
以![]() 的速度沿
的速度沿![]() 边向点
边向点![]() 运动,如果
运动,如果![]() 、
、![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 的长.
的长.
(![]() )当点
)当点![]() 运动到点
运动到点![]() 时,
时, ![]() 、
、![]() 同时停止运动.在运动过程中,是否存在
同时停止运动.在运动过程中,是否存在![]() 的值,使得
的值,使得![]() 、
、![]() 、
、![]() 的面积都相等,若存在,求出
的面积都相等,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(![]() )当运动
)当运动![]() 时,
时, ![]() 点停止运动,
点停止运动, ![]() 点以原速立即向
点以原速立即向![]() 点返回,在返回的过程中,
点返回,在返回的过程中, ![]() 是否能平分
是否能平分![]() ?若能,求出点
?若能,求出点![]() 运动的时间;若不能,请说明理由.
运动的时间;若不能,请说明理由.
参考答案:
【答案】见解析.
【解析】试题分析:(1)根据题意,易求BP的长,再利用勾股定理求得PQ的长即可;(2)用t表示出![]() 和
和![]() ,根据面积相等列出方程,解方程即可解决问题;(3)若
,根据面积相等列出方程,解方程即可解决问题;(3)若![]() 平分
平分![]() ,作
,作![]() 于点
于点![]() (如图所示),利用HL证明
(如图所示),利用HL证明![]() ≌
≌![]() ,根据全等三角形的性质可得
,根据全等三角形的性质可得![]() ,再用AAS证明
,再用AAS证明![]() ≌
≌![]() ,设
,设![]() ,则
,则![]() ,
, ![]() .在
.在![]() 中,根据勾股定理列出方程,解方程求得x的值,继而求得t值.
中,根据勾股定理列出方程,解方程求得x的值,继而求得t值.
试题解析:
(![]() )
)![]() 时,
时, ![]() ,
, ![]() ,
,
∴![]() .
.
∴![]() .
.
(![]() )∵
)∵![]() ,
, ![]() ,
, ![]() .
.
∴![]() .
.
![]()
![]() .
.
若![]() .
.
即![]() .
.
解得![]() .
.
∴不存在.
(![]() )当
)当![]() 时,
时, ![]() ,
, ![]() .
.
如图所示,若![]() 平分
平分![]() ,作
,作![]() 于点
于点![]() .
.
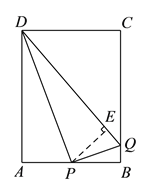
∴![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,
∴![]() ≌
≌![]() .
.
∴![]() .
.
在![]() 和
和![]() 中,
中,
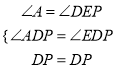 ,
,
∴![]() ≌
≌![]() .
.
∴![]() .
.
设![]() ,则
,则![]() .
.
![]() .
.
在![]() 中,
中, ![]() .
.
即![]() .
.
解得![]() .
.
∴![]() .
.
∴![]() 又走了
又走了![]() ,
,
∵原来运动![]() .
.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验与探究:
(
 )如图,直线
)如图,直线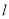 为第一、三象限的角平分线,观察易知
为第一、三象限的角平分线,观察易知 关于直线
关于直线 的对称点
的对称点 的坐标为
的坐标为 ,请在图中分别标明
,请在图中分别标明 、
、 关于直线
关于直线 的对称点
的对称点 、
、 的位置,并写出他们的坐标:
的位置,并写出他们的坐标:  __________、
__________、 __________.
__________.(
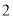 )结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点
)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点 关于第一、三象限的角平分线
关于第一、三象限的角平分线 的对称点
的对称点 的坐标为__________ (不必证明).
的坐标为__________ (不必证明).(
 )已知两点
)已知两点 、
、 ,在直线
,在直线 上是否存在一点
上是否存在一点 ,使点
,使点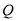 到
到 、
、 两点的距离之和最小,并求出最小距离.
两点的距离之和最小,并求出最小距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,
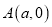 ,
, 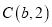 ,且满足
,且满足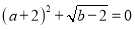 ,过
,过 作
作 轴于
轴于 .
.(
 )求
)求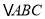 的面积.
的面积.(
 )在
)在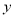 轴上是否存在点
轴上是否存在点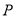 ,使
,使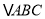 和
和 的面积相等?若存在,求出
的面积相等?若存在,求出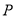 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.(
 )动点
)动点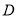 从点
从点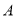 出发,以每秒
出发,以每秒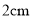 的速度沿射线
的速度沿射线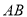 运动,如果在运动过程中
运动,如果在运动过程中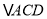 为等腰三角形,求出点
为等腰三角形,求出点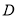 运动的时间.
运动的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校7年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.

(1)在平面直角坐标系中画出探险路线图;
(2)分别写出A、B、C、D、P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )

A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于( )

A.90° B.75° C.70° D.60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )

A. (a+b)2=a2+2ab+b2
B. (a﹣b)2=a2﹣2ab+b2
C. a2﹣b2=(a+b)(a﹣b)
D. (a+2b)(a﹣b)=a2+ab﹣2b2
相关试题

