【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )

A.1个 B.2个 C.3个 D.4个
参考答案:
【答案】B
【解析】
试题分析:根据全等三角形的判定定理,可以推出①②③为条件,④为结论,依据是“SAS”;①②④为条件,③为结论,依据是“SSS”.
解:当①②③为条件,④为结论时:
∵∠A′CA=∠B′CB,
∴∠A′CB′=∠ACB,
∵BC=B′C,AC=A′C,
∴△A′CB′≌△ACB,
∴AB=A′B′,
当①②④为条件,③为结论时:
∵BC=B′C,AC=A′C,AB=A′B′
∴△A′CB′≌△ACB,
∴∠A′CB′=∠ACB,
∴∠A′CA=∠B′CB.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数的平方是正数,则这个数是( )
A.正数B.负数C.不为零的数D.非负数
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的解题过程:
计算:(﹣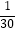 )÷(
)÷(  ﹣
﹣  +
+  ﹣
﹣ 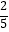 )
)
方法一:原式=(﹣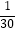 )÷[(
)÷[(  +
+  )﹣(
)﹣(  +
+ 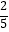 )]=(﹣
)]=(﹣ 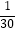 )÷(
)÷(  ﹣
﹣  )=﹣
)=﹣ 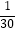 ×3=﹣
×3=﹣ 
方法二:原式的倒数为( ﹣
﹣  +
+  ﹣
﹣ 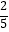 )÷(﹣
)÷(﹣ 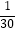 )=(
)=(  ﹣
﹣  +
+  ﹣
﹣ 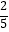 )×(﹣30)=﹣20+3﹣5+12=﹣10
)×(﹣30)=﹣20+3﹣5+12=﹣10
故原式=﹣
通过阅读以上解题过程,你认为哪种方法更简单,选择合适的方法计算下题:
(﹣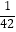 )÷(
)÷(  ﹣
﹣ 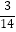 +
+  ﹣
﹣  ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD与四边形CEFG是两个正方形,边长分别为a、b.其中B、C、E在一条直线上,G在线段CD上.三角形AGE的面积为S.
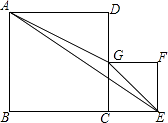
(1)①当a=5,b=3时,求S的值;
②当a=7,b=3时,求S的值;
(2)从以上结果中,请你猜想S与a、b中的哪个量有关?用字母a,b表示S,并对你的猜想进行证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个样本的50个数据分别落在4个组内,第1、2、3组数据的个数分别是7、8、15,则第4组数据的频率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )

A.6 B.8 C.9 D.10
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数:①3、4、5 ②4、5、6 ③2.5、6、6.5 ④8、15、17,其中是勾股数的有( )
A. 4组 B. 3组 C. 2组 D. 1组
相关试题

