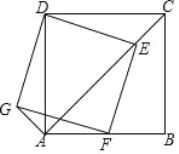
【题目】如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE、EF为邻边作矩 形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值;
(3)若F恰为AB中点,连接DF交AC于点M,求ME的长.
参考答案:
【答案】(1)见解析;(2)AG+ AE=4![]() ;(3)EM=
;(3)EM=![]() .
.
【解析】
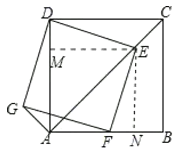
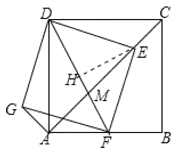
(1)如图,作EM⊥AD于M,EN⊥AB于N.只要证明△EMD≌△ENF即可解决问题;
(2)只要证明△ADG≌△CDE,可得AG=EC即可解决问题;
(3)如图,作EH⊥DF于H.想办法求出EH,HM即可解决问题;
解:(1)如图,作EM⊥AD于M,EN⊥AB于N.
∵四边形ABCD是正方形,
∴∠EAD=∠EAB,
∵EM⊥AD于M,EN⊥AB于N,
∴EM=EN,
∵∠EMA=∠ENA=∠DAB=90°,
∴四边形ANEM是矩形,
∴∠MEN=∠DEF=90°,
∴∠DEM=∠FEN,
∵∠EMD=∠ENF=90°,
∴△EMD≌△ENF,
∴ED=EF,
∵四边形DEFG是矩形,
∴四边形DEFG是正方形;
(2)∵四边形DEFG是正方形,四边形ABCD是正方形,
∴DG=DE,DC=DA=AB=4,∠GDE=∠ADC=90°,
∴∠ADG=∠CDE,
∴△ADG≌△CDE,
∴AG=CE,
∴AE+AG=AE+EC=AC=![]() AD=4
AD=4![]() ;
;
(3)如图,作EH⊥DF于H.
∵四边形ABCD是正方形,
∴AB=AD=4,AB∥CD,
∵F是AB中点,
∴AF=FB
∴DF=![]() ,
,
∵△DEF是等腰直角三角形,EH⊥AD,
∴DH=HF,
∴EH=![]() DF=
DF=![]() ,
,
∵AF∥CD,
∴△AFM∽△CDM,
∴AF:CD=FM:MD=1:2,
∴FM=![]() ,
,
∴HM=HFFM=![]() ,
,
在Rt△EHM中,EM=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】考试前夕,为“连粽连中”的吉祥寓意,某校食堂购进甲、乙两种粽子520个,其中甲种粽子花费600元,乙种粽子花费800元,已知甲种粽子单价比乙种粽子单价高20%,乙种粽子的单价是多少元?甲、乙两种粽子各购买了多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数是( )
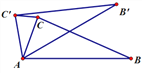
A. 70° B. 35° C. 40° D. 90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点E、F分别在AB、BC上,且AE=BF=1,CE、DF交于点O,下列结论:①∠DOC=90°,②OC=OE,③CE=DF,④tan∠OCD=
 ,⑤S△DOC=S四边形EOFB中,正确的有( )
,⑤S△DOC=S四边形EOFB中,正确的有( )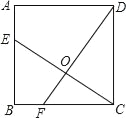
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】“奔跑吧,兄弟!”节目组预设计一个新游戏:“奔跑”路线A、B、C、D四地,如图A、B、C三地在同一直线上,D在A北偏东30°方向,在C北偏西45°方向,C在A北偏东75°方向,且BD=BC=40m,从A地到D地的距离是_____m.
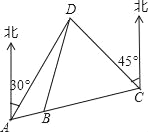
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生及家长就校园安全知识的了解程度进行了随机抽样调查,并绘制成如图所示的两幅统计图,请根据统计图中的信息,解答下列问题:
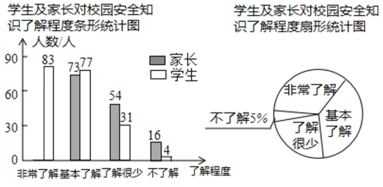
 参与调查的学生及家长共有 人;
参与调查的学生及家长共有 人;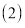 在扇形统计图中,求“基本了解"所对应的扇形的圆心角的度数;
在扇形统计图中,求“基本了解"所对应的扇形的圆心角的度数; 在条形统计图中,“非常了解”所对应的学生人数是______人 并补全条形统计图.
在条形统计图中,“非常了解”所对应的学生人数是______人 并补全条形统计图. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC和BD交于点O,分别过点B、C作BE∥AC,CE∥BD,BE与CE交于点E.
(1)求证:四边形OBEC是矩形;
(2)当∠ABD=60°,AD=2
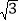 时,求∠EDB的正切值.
时,求∠EDB的正切值.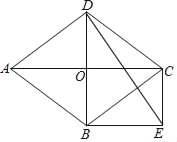
相关试题

