Question

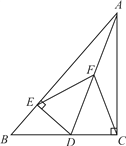
【题目】如图，在Rt△ABC中，∠ACB=90°，D是边BC上一点，DE⊥AB于点E，点F是线段AD上一点，连结EF、CF.

（1）若AD平分∠BAC，求证：EF=CF.

（2）若点F是线段AD的中点，试猜想线段EF与CF的大小关系，并加以证明.

（3）在（2）的条件下，若∠BAC=45°，AD=6，直接写出C、E两点间的距离.

Answer 1

【答案】（1）证明见解析；（2）EF=CF.理由见解析；（3）.

【解析】试题分析：（1）由AD平分∠BAC，DE⊥AB，∠ACB=90°可得：∠1 =∠2，∠1+∠3=90°，∠2+∠4=90°，DE= DC，则∠3=∠4，则在△DEF≌△DCF，再根据全等三角形的性质可得出EF=CF；（2）在Rt△AED和Rt△ACD中，由点F是线段AD的中点可得： ， ，所以EF=CF；（3）由AD=6，EF＝CF＝ AD＝AF＝DF＝3可得：∠DFE＝2∠FAE,∠CFD＝2∠CAF,所以∠EFC＝2∠CAE＝90°，即△CEF是直角三角形，所以CE＝ ；

试题解析：

（1）如图所示：

∵AD平分∠BAC，DE⊥AB，∠ACB=90°，

∴∠1 =∠2，∠1+∠3=90°，∠2+∠4=90°，DE= DC.

∴∠3=∠4.

∵DF = DF，

∴△DEF≌△DCF.

∴EF=CF.

（2）EF=CF. （只写结论给1分）

在Rt△AED和Rt△ACD中，

∵点F是线段AD的中点，

∴， ，

∴EF=CF. \

（3）.