【题目】如图,四边形ABCD是边长为a的正方形,点G、E分别是边AB、BC的中点,∠AEF=90°,且EF交正方形外角的平方线CF于点F.
(1)证明:△AGE≌△ECF;
(2)求△AEF的面积.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)根据正方形的性质,易证得AG=EC,∠AGE=∠ECF=135°;再加上(1)得出的相等角,可由ASA判定两个三角形全等;
(2)在Rt△ABE中,根据勾股定理易求得AE2;由(2)的全等三角形知:AE=EF,即△AEF是等腰Rt△,因此其面积为AE2的一半,由此得解.
试题解析:(1)证明:∵G,E分别是正方形ABCD的边AB,BC的中点,∴AG=GB=BE=EC,且∠AGE=180°﹣45°=135°;
又∵CF是∠DCH的平分线,∴∠DCF=∠FCH=45°,∠ECF=90°+45°=135°;
在△AGE和△ECF中,∵AG=EC,∠AGE=∠ECF=135°,∠GAE=∠FEC;
∴△AGE≌△ECF;
(2)解:由△AGE≌△ECF,得AE=EF;
又∵∠AEF=90°,∴△AEF是等腰直角三角形;
∵AB=a,E为BC中点,∴BE=![]() BC=
BC=![]() AB=
AB=![]() a,根据勾股定理得:AE=
a,根据勾股定理得:AE=![]() =
=![]() a,∴S△AEF=
a,∴S△AEF=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件为必然事件的是( )
A. 任意买一张电影票,座位号是偶数
B. 打开电视机,正在播放动画片
C. 两角及一边对应相等的两个三角形全等
D. 三根长度为2cm、3cm、5cm的木棒首尾相接能摆成三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.
(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°
①求证:AD=BE;
②求∠AEB的度数.
(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=
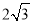 CM+
CM+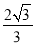 BN.
BN.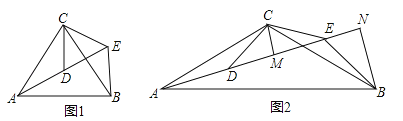
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场投入13800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价
成本价
销售价(元/箱)
甲
24
36
乙
33
48
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列两个图形一定相似的是( )
A.矩形B.有一个内角为100°的等腰三角形
C.直角三角形D.菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人购进一批苹果,到市场零售,已知销售额y(元)与卖出的苹果数量x(千克)的关系如表所示:则y与x之间的关系式为__________
数量x(千克)
2
3
4
5
…
销售额y(元)
7.2
10.8
14.4
18.0
…
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a3a=a3
B.(2a+b)2=4a2+b2
C.a8b÷a2=a4b
D.(﹣3ab3)2=9a2b6
相关试题

