【题目】已知:a、b、c满足a=-b,|a+1|+(c-4)2=0,请回答问题:
(1)请求出a、b、c的值;
(2)a、b、c所对应的点分别为A、B、C,P为数轴上一动点,其对应的数为x,若点P在线段BC上时,请化简式子:|x+1|-|1-x|+2|x-4|(请写出化简过程);
![]()
(3)若点P从A点出发,以每秒2个单位长度的速度向右运动,试探究当点P运动多少秒时,PC=3PB?
参考答案:
【答案】(1)a=-1, b=1,c=4;(2)-2x+10;(3)![]() 或
或![]() 秒
秒
【解析】试题分析:
(1) 利用“若几个非负数之和为零则每一个非负数均为零”这一结论,可以得到a与c的值. 利用已知条件容易得到b的值.
(2) 根据“点P在线段BC上”可以得到x的取值范围. 根据x的取值范围,可以依次确定待化简式子中绝对值符号内的整式值的符号,再根据绝对值的代数意义去掉相应的绝对值符号,然后合并同类项即可得出答案.
(3) 设点P的运动时间为t秒. 分析题意可知,要想得到符合题意的运动时间,就需要获得线段PC与线段PB的长关于运动时间t的表达式. 对于线段PC的表达式,可以通过PC=AC-AP的关系得到. 线段AC的长易知;由于点P从点A出发沿直线向右运动,所以线段AP的长代表了点P的运动路程. 根据“路程等于速度乘以时间”这一等量关系,可以用t表示出线段AP的长. 对于线段PB的表达式,则需要按照点P与点B的相对位置进行讨论. 当点P在点B的左侧时,可根据PB=AB-AP获得线段PB的表达式;当点P在点B的右侧时,可根据PB=AP-AB获得线段PB的表达式. 在获得上述表达式后,利用等量关系PC=3PB列出方程求解时间t即可.
试题解析:
(1) 因为![]() ,所以a+1=0,c-4=0,即a=-1,c=4.
,所以a+1=0,c-4=0,即a=-1,c=4.
因为a=-b,a=-1,所以b=-a=-(-1)=1.
综上所述,a=-1,b=1,c=4.
(2) 因为点P在线段BC上,b=1,c=4,所以![]() .
.
因为![]() ,所以x+1>0,
,所以x+1>0, ![]() ,
, ![]() .
.
当x+1>0时, ![]() ;
;
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() .
.
因此,当点P在线段BC上(即![]() )时,
)时,
![]()
=![]()
= ![]()
=![]() .
.
(3) 设点P的运动时间为t秒.
因为点P从A点出发,以每秒2个单位长度的速度向右运动,所以AP=2t.
因为点A对应的数为-1,点C对应的数为4,所以AC=4-(-1)=5.
因为PC=3PB,所以PC>PB. 故点P不可能在点C的右侧.
因此,PC=AC-AP.
因为AP=2t,AC=5,所以PC=AC-AP=5-2t.
分析本小题的题意,点P与点B的位置关系没有明确的限制,
故本小题应该对以下两种情况分别进行求解.
①点P在点B的左侧,如下图.
![]()
因为点A对应的数为-1,点B对应的数为1,所以AB=1-(-1)=2.
因为AP=2t,AB=2,所以PB=AB-AP=2-2t.
因为PC=3PB,PC=5-2t,PB=2-2t,所以5-2t=3(2-2t).
解这个关于t的一元一次方程,得 ![]() .
.
②点P在点B的右侧,如下图.
![]()
因为AP=2t,AB=2,所以PB=AP-AB=2t-2.
因为PC=3PB,PC=5-2t,PB=2t-2,所以5-2t=3(2t-2).
解这个关于t的一元一次方程,得 ![]() .
.
综上所述,当点P运动![]() 或
或![]() 秒时,PC=3PB.
秒时,PC=3PB.
-
科目: 来源: 题型:
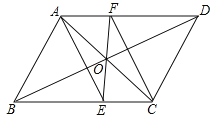
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD交于点O,EF过点O且与BC、AD分别交于点E、F.试猜想线段AE、CF的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两相似三角形的面积之比为9∶16,若小三角形的周长为6厘米,则大三角形的周长为_______厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分母中含有的方程叫做分式方程;分式方程的识别标准是:一是;二要中含有未知数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】a3a4a+(a2)4+(﹣2a4)2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系.根据图像提供的信息,解答下列问题:
(1)求线段AB所在直线的函数关系式,并求甲、乙两地的距离;
(2)求两车的速度;
(3)求点C的坐标,并写出点C的实际意义.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某一出租车一天下午以新合作超市为出发地在东西方向营运,向东为正,向西为负,行车里程(单位km),依先后次序记录如下:+7,-4,-6,+4,-8,+6,-3,-7,-5,+10.
⑴将最后一名乘客送到目的地,出租车离出发点多远?在新合作的什么方向?
⑵若每千米按2.4元收费,该司机一个下午的收入多少?
相关试题

