【题目】小明从二次函数y=ax2+bx+c的图象(如图)中观察
得出了下面五条信息:①c<0;②abc>0;③a-b+c>0;④2a-3b=0;⑤c-4b>0.
你认为其中正确的信息是_________________.(只填序号)

参考答案:
【答案】①②③⑤
【解析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答:解:因为函数图象与y轴的交点在y轴的负半轴可知,
所以c<0,∴①正确;
∵函数图象开口向上,
∴a>0,由①知,c<0,
由函数的对称轴在x的正半轴上可知,x=-![]() >0,故b<0,故abc<0,∴②正确;
>0,故b<0,故abc<0,∴②正确;
∵把x=-1代入函数解析式,由函数的图象可知,x=-1时,y>0即a-b+c>0,∴③正确;
∵a>0,b<0,
∴2a>3b,
∴2a-3b>0,∴④错误;
∵函数的对称轴为x=-![]() >0,a>0,
>0,a>0,
∴-b<2a,
∴2a+b>0,∴⑤正确;
其中正确信息的有①②③⑤.
-
科目: 来源: 题型:
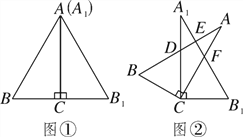
查看答案和解析>>【题目】将两块相同的含30°角的直角三角板按图①的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图②的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
(1)当旋转角等于20°时,∠BCB1=________度;
(2)当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形ABCD中,AD∥BC,∠ABC=∠DCB,AB=DC。
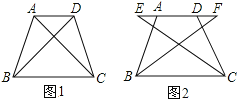
(1)求证:AC=DB;
(2)如图2,E、F两点同时从A、D出发在直线AD上以相同的速度反向而行,BF和CE会相等吗?请证明你的结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒
 cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )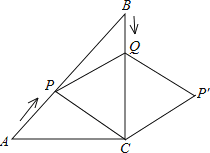
A.
 B.2 C.2
B.2 C.2 D.3
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】探究证明:
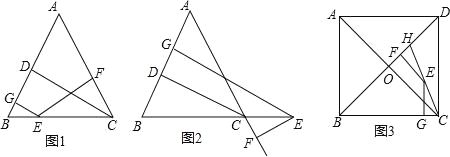
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,BC∥OA,∠B=∠A=100°,点E、F在BC上,OE平分∠BOF,且∠FOC=∠AOC,下列结论中正确的是___________:

①OB∥AC ②∠EOC=45°
③∠OCB:∠OFB=1:3 ④若∠OEB=∠OCA,则∠OCA=60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD,四边形BEFG均为正方形,连接AG,CE.试说明:
(1)AG=CE;
(2)AG⊥CE.

相关试题

