【题目】如图1,四边形ABCD中,AD∥BC,∠ABC=∠DCB,AB=DC。
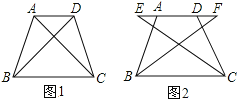
(1)求证:AC=DB;
(2)如图2,E、F两点同时从A、D出发在直线AD上以相同的速度反向而行,BF和CE会相等吗?请证明你的结论。
参考答案:
【答案】(1)证明见解析(2)BF=CE
【解析】试题分析:
(1)由∠ABC=∠DCB,AB=DC结合BC=CB即可证得:△ABC≌△DCB,从而可得AC=DB;
(2)由题意可得AE=DF,从而可得AF=DE,由AD∥BC结合∠ABC=∠DCB,易得∠BAD=∠CDA,再结合AB=DC即可证得△BAF≌△CDE,从而可得BF=CE.
试题解析:
(1)在△ABC和△DCB中,
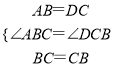 ,
,
∴△ABC≌△DCB(SAS),
∴AC=DB;
(2)BF=CE,理由如下:
由题意可得:AE=DF,
∴AF=DE,
∵AD∥BC,
∴∠BAD+∠ABC=180°,∠CDA+∠DCB=180°,
∵∠ABC=∠DCB,
∴∠BAD=∠CDA,
在△BAF和△CDE中,
 ,
,
∴△BAF≌△CDE(SAS),
∴BF=CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )

A. (6,0) B. (6,3) C. (6,5) D. (4,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BD为△ABC的的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )
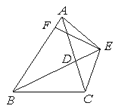
A.①②③ B.①③④ C.①②④ D.①②③④
-
科目: 来源: 题型:
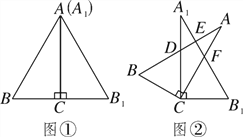
查看答案和解析>>【题目】将两块相同的含30°角的直角三角板按图①的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图②的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
(1)当旋转角等于20°时,∠BCB1=________度;
(2)当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒
 cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )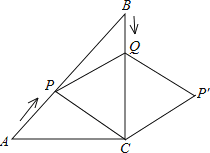
A.
 B.2 C.2
B.2 C.2 D.3
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】小明从二次函数y=ax2+bx+c的图象(如图)中观察
得出了下面五条信息:①c<0;②abc>0;③a-b+c>0;④2a-3b=0;⑤c-4b>0.
你认为其中正确的信息是_________________.(只填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】探究证明:
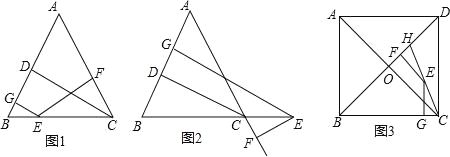
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .
相关试题

