搜索
【题目】计算：
（1）﹣1+ 
﹣ 
+ 
；
（2）（﹣2）÷ 
×（﹣3）；
（3）﹣24×（﹣ 
+ 
﹣ 
）；
（4）﹣5﹣（﹣11）+2 ﹣（﹣ 
）．
参考答案：
【答案】
（1）解：原式=﹣1+ 
﹣ 
+ 
=﹣ 
（2）解：原式=2×3×3=18
（3）解：原式=20﹣9+2=13
（4）解：原式=﹣5+11+2 
+ 
=6+3=9
【解析】（1）原式通分并利用同分母分数的加减法则计算即可得到结果；（2）原式从左到右依次计算即可得到结果；（3）原式利用乘法分配律计算即可得到结果；（4）原式利用减法法则变形计算，即可得到结果．
【考点精析】根据题目的已知条件，利用有理数的四则混合运算的相关知识可以得到问题的答案，需要掌握在没有括号的不同级运算中，先算乘方再算乘除，最后算加减．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用“⊕”定义一种新运算：对于任意有理数a和b，规定a⊕b＝ab2+2ab+a．
如：1⊕3＝1×32+2×1×3+1＝16．
（1）求（﹣2）⊕3的值；
（2）若（a⊕3）⊕1＝128，求a的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市地铁2号线已开工，全长约382000m，将382000科学记数法表示应为（ ）
A. 0.382x106 B. 3.82x105 C. 38.2x104 D. 382x103
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，抛物线y=﹣
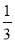x2﹣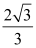
x+3与x轴交于A、B两点（点A在点B的右侧），交y轴于点C，点D的坐标为（0，﹣1），直线AD交抛物线于另一点E，点P是第二象限抛物线上的一点，作PQ∥y轴交直线AE于Q，作PG⊥AD于G，交x轴于点H（1）求线段DE的长；
（2）设d=PQ﹣
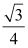PH，当d的值最大时，在直线AD上找一点K，使PK+
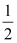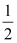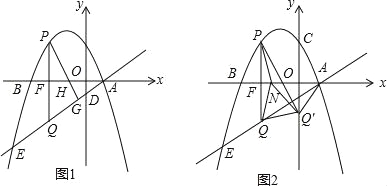
EK的值最小，求出点K的坐标和PK+EK的最小值；（3）如图2，当d的值最大时，在x轴上取一点N，连接PN，QN，将△PNQ沿着PN翻折，点Q的对应点为Q′，在x轴上是否存在点N，使△AQQ′是等腰三角形？若存在，求出点N的坐标，若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列因式分解正确的是（ ）
A. -a2+a3 =-a2(1+a) B. 2x-4y+2=2(x-2y)
C. 5x2+5y2=5(x+y)2 D. a2-8a+16=(a-4)2
-
科目： 来源： 题型：
查看答案和解析>>【题目】若x2-x+M=(x-4)·N，则M、N分别为（ ）
A. -12，x+3 B. 20，x-5 C. 12，x-3 D. -20，x+5
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）﹣1+
﹣ 
+ 
；
（2）（﹣2）÷
×（﹣3）；
（3）﹣24×（﹣
+ 
﹣ 
）；
（4）﹣5﹣（﹣11）+2 ﹣（﹣ 
）．
相关试题
