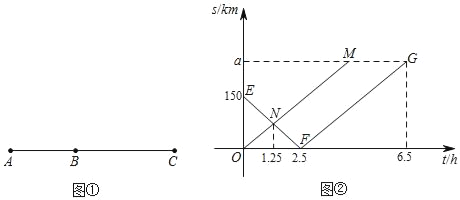
【题目】如图①,A、B、C三地依次在一直线上,两辆汽车甲、乙分别从A、B两地同时出发驶向C地,如图②,是两辆汽车行驶过程中到C地的距离s(km)与行驶时间t(h)的关系图象,其中折线段EF﹣FG是甲车的图象,线段OM是乙车的图象.
(1)图②中,a的值为 ;点M的坐标为 ;
(2)当甲车在乙车与B地的中点位置时,求行驶的时间t的值.
参考答案:
【答案】(1)240,(4,240);(2)t的值为2(h).
【解析】
(1)先求出直线EF的解析式,进而求出点N的坐标,再根据点N的坐标求出直线OM的解析式,进而求出直线FG的解析式,即可得出a的值;
(2)根据乙车行驶的路程与行驶时间的关系求解即可.
(1)设EF的解析式为y=k1x+150,
因为直线EF经过(2.5,0),所以2.5k1+150=0,解得k1=﹣60,
所以EF的解析式为y=﹣60x+150;
因为点M在EF上,所以点N的纵坐标为:﹣60×1.25+150=75,
因为点N的坐标为(1.25,75);
设直线OM的解析式为y=k2x,因为直线OM经过点N,所以1.25k2=75,解得k2=60,
所以直线OM的解析式为y=60x,
所以直线FG的解析式为y=60x﹣150,
所以点G的纵坐标,即a=60×6.5﹣150=240,
所以点M的横坐标为240÷60=4,即点M的坐标为(4,240).
故答案为:240;(4,240);
(2)由点M的坐标可知乙车的速度为240÷4=60(千米/时)
当甲车在乙车与B地的中点位置时,行驶的时间t的值为![]() =2(h).
=2(h).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.
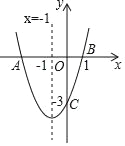
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )
A. m≤2或m≥3 B. m≤3或m≥4 C. 2<m<3 D. 3<m<4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,则水面下降1m时,水面宽度增加_____m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某店只销售某种进价为40元/kg的产品,已知该店按60元kg出售时,每天可售出100kg,后来经过市场调查发现,单价每降低1元,则每天的销售量可增加10kg.
(1)若单价降低2元,则每天的销售量是_____千克,每天的利润为_____元;若单价降低x元,则每天的销售量是_____千克,每天的利润为______元;(用含x的代数式表示)
(2)若该店销售这种产品计划每天获利2240元,单价应降价多少元?
(3)当单价降低多少元时,该店每天的利润最大,最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 于点
于点 ,
, 和
和 的角平分线相交于点
的角平分线相交于点 ,
, 为边
为边 的中点,
的中点, ,则
,则 ( )
( )
A.125°B.145°C.175°D.190°
相关试题

