【题目】写出一个抛物线开口向下,与y轴交于(0,2)点的函数表达式 .
参考答案:
【答案】y=﹣x2+x+2
【解析】解:∵开口向下,
∴y=ax2+bx+c中a<0,
∵与y轴交于(0,2)点,
∴c=2,
∴抛物线的解析式可以为:y=﹣x2+x+2(答案不唯一).
故答案为:y=﹣x2+x+2(答案不唯一).
首先根据开口向下得到二次项系数小于0,然后根据与y轴的交点坐标的纵坐标为2得到c值即可得到函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ACD和Rt△BEC中,若AD=BE,DC=EC,则不正确的结论是( )

A. Rt△ACD和Rt△BCE全等 B. OA=OB
C. E是AC的中点 D. AE=BD
-
科目: 来源: 题型:
查看答案和解析>>【题目】从2开始的连续偶数相加,它们和的情况如下表:
加数的个数(n)
和(S)
1
2=1×2
2
2+4=6=2×3
3
2+4+6=12=3×4
4
2+4+6+8=20=4×5
5
2+4+6+8+10=30=5×6
…
…
(1)根据表中的规律,直接写出2+4+6+8+10+12+14=________
(2)根据表中的规律猜想:S=2+4+6+8+…+2n=___________(用n的代数式表示);
(3)利用上题中的公式计算102+104+106+…+200的值(要求写出计算过程).
-
科目: 来源: 题型:
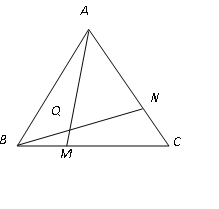
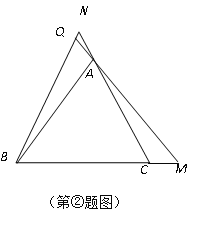
查看答案和解析>>【题目】学完“等腰三角形”一章后,老师布置了一道思考题:如图,点M,N分别在正三角形
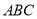 的
的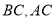 边上,且
边上,且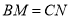 ,
, 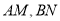 交于点
交于点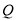 .求证:
.求证: 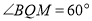 .
.(1)请你完成这道思考题;
(2)做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“
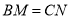 ”与“
”与“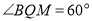 ”的位置交换,得到的是否仍是真命题?
”的位置交换,得到的是否仍是真命题?②若将题中的点
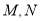 分别移动到
分别移动到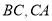 的延长线上,是否仍能得到
的延长线上,是否仍能得到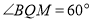 ?
?……
请你作出判断,在下列横线上填写“是”或“否”:① ;② ;选择一个给出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】度、分、秒换算:27.24°=_____°_____′_____″.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°.
(1)作∠CAB的平分线,交BC边于点D(用尺规作图,保留作图痕迹,不要求写作法和证明);
(2)求S△ACD:S△ABC的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:(1)x2﹣6x+5=0(配方法) (2)(x+1)2=6x+6.
相关试题

