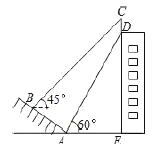
【题目】如图,某建筑物的顶部有一块标识牌![]() ,小明在斜坡上
,小明在斜坡上![]() 处测得标识牌顶部
处测得标识牌顶部![]() 的仰角为
的仰角为![]() ,沿斜坡走下来在地面
,沿斜坡走下来在地面![]() 处测得标识牌底部
处测得标识牌底部![]() 的仰角为60°,已知斜坡
的仰角为60°,已知斜坡![]() 的坡角为30°,
的坡角为30°,![]() 米. 则标识牌
米. 则标识牌![]() 的高度是米__________.
的高度是米__________.
参考答案:
【答案】![]()
【解析】
过点B作BM⊥EA的延长线于点M,过点B作BN⊥CE于点N,通过解直角三角形可求出BM,AM,CN,DE的长,再结合CD=CN+ENDE即可求出结论.
解:过点B作BM⊥EA的延长线于点M,过点B作BN⊥CE于点N,如图所示.
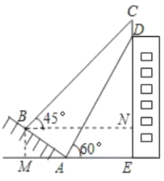
在Rt△ABM中,AB=10米,∠BAM=30°,
∴AM=ABcos30°=5![]() (米),BM=ABsin30°=5(米).
(米),BM=ABsin30°=5(米).
在Rt△ADE中,AE=10(米),∠DAE=60°,
∴DE=AEtan60°=10![]() (米).
(米).
在Rt△BCN中,BN=AE+AM=10+5![]() (米),∠CBN=45°,
(米),∠CBN=45°,
∴CN=BNtan45°=10+5![]() (米),
(米),
∴CD=CN+ENDE=10+5![]() +510
+510![]() =155
=155![]() (米).
(米).
故答案为:155![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,二次函数
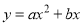 与一次函数
与一次函数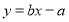 的图像可能是( )
的图像可能是( )A.
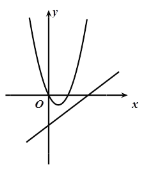 B.
B.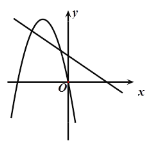
C.
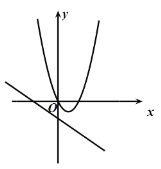 D.
D.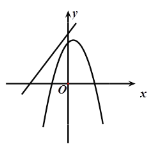
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
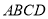 中,
中,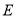 是
是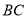 边上的一点,
边上的一点,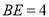 ,
,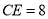 ,将正方形边
,将正方形边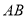 沿
沿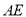 折叠到
折叠到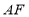 ,延长
,延长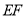 交
交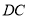 于
于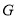 .连接
.连接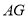 ,现在有如下四个结论:①
,现在有如下四个结论:①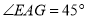 ;②
;②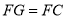 ;③
;③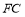 ∥
∥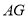 ;④
;④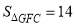 ; 其中结论正确的个数是( )
; 其中结论正确的个数是( )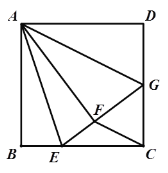
A.1B.2
C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, ,
, 为边
为边 上一动点,
上一动点, 于点
于点 ,
, 于点
于点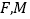 为
为 的中点,则
的中点,则 的最小值为( )
的最小值为( )
A.
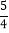 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=4﹣x与双曲线y
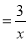 交于A,B两点,过B作直线BC⊥y轴,垂足为C,则以OA为直径的圆与直线BC的交点坐标是_____.
交于A,B两点,过B作直线BC⊥y轴,垂足为C,则以OA为直径的圆与直线BC的交点坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“大千故里,文化内江”,我市某中学为传承大千艺术精神,征集学生书画作品.王老师从全校20个班中随机抽取了
 4个班,对征集作品进行了数量分析统计,绘制了如下两幅不完整的统计图.
4个班,对征集作品进行了数量分析统计,绘制了如下两幅不完整的统计图.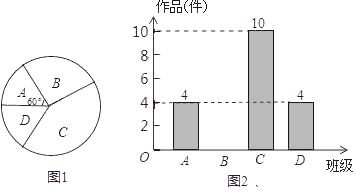
(1)王老师采取的调查方式是 (填“普查”或“抽样调査”),王老师所调查的4个班共征集到作品 件,并补全条形统计图;
(2)在扇形统计图中,表示
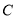 班的扇形周心角的度数为 ;
班的扇形周心角的度数为 ;(3)如果全校参展作品中有4件获得一等奖,其中有1名作者是男生,3名作者是女生.现要从获得一等奖的作者中随机抽取两人去参加学校的总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】樱桃是我市的特色时令水果.一上市,水果店的老板用2400元购进一批樱桃,很快售完;老板又用3700元购进第二批樱桃,进价比第一批每千克少了11元,所购件数是第一批2的倍.
(1)第一批樱桃进价是每千克多少元?
(2)老板以每千克50元的价格销售第二批樱桃,售出80%后,为了尽快售完,剩下降价促销、要使得第二批樱桃的销售利润不低于1100元,剩余的樱桃每千克最多降价多少元销售?
相关试题

