【题目】最近,“校园安全”受到全社会的广泛关注,重庆八中对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如下两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)扇形统计图中“基本了解”部分所对应扇形的圆心角为度;请补全条形统计图;
(2)若达到“了解”程度的人中有1名男生2名女生,达到“不了解”的程度的人中有1名男生和1名女生,若分别从达到“了解”程度和“不了解”的人中分别抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1名男生和1名女生的概率.
参考答案:
【答案】
(1)120,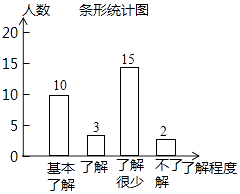
(2)解:设了解的学生为(A男,A女,A女),不了解的为(B男,B女),
则出现的所有可能性为:(A男,B男)、(A男、B女)、(A女,B男)、(A女,B女)、(A女,B男)、(A女,B女),
∴恰好抽到1名男生和1名女生的概率是:![]()
![]() ,
,
即恰好抽到1名男生和1名女生的概率是 ![]() .
.
【解析】解:(1)由题意可得,
本次调查的学生有:15÷50%=30(人),
扇形统计图中“基本了解”部分所对应扇形的圆心角为:360°× ![]() =120°,
=120°,
了解的有:30﹣10﹣15﹣2=3(人),
(1)圆心角=360° ![]() 百分比;条形统计图的补全关键是求出所缺部分的数量,部分
百分比;条形统计图的补全关键是求出所缺部分的数量,部分![]() 百分比=总数,具体量=样本容量
百分比=总数,具体量=样本容量 ![]() 相应百分比;(2)
相应百分比;(2)
关注的结果为3个,机会均等所谓结果有6个,代入概率公式即可得概率为0.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B=50°,P 为 AB 中点,点 M 为射线 AC 上(不与点 A 重合)的任意一点,连接 MP, 并使MP 的延长线交射线BD 于点N,设∠BPN=α.

(1)求证:△APM≌△BPN;
(2)当 MN=2BN 时,求α的度数;
(3)若△BPN 为锐角三角形时,直接写出α的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.

(1,1),(3,1),(1,3),(1,1);
(-1,3),(-1,5),(-3,3),(-1,3);
(-5,1),(-3,-1),(-3,1),(-5,1);
(-1,-1),(1,-1),(-1,-3),(-1,-1).
(1)观察所得的图形,你觉得它像什么?
(2)求出这四个图形的面积和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图1菱形ABCD,∠ABC=60°,边长为 3,在菱形内作等边三角形△AEF,边长为2
 ,点E,点F,分别在AB,AC上,以A为旋转中心将△AEF顺时针转动,旋转角为α,如图2
,点E,点F,分别在AB,AC上,以A为旋转中心将△AEF顺时针转动,旋转角为α,如图2
(1)在图2中证明BE=CF;
(2)若∠BAE=45°,求CF的长度;
(3)当CF=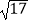 时,直接写出旋转角α的度数.
时,直接写出旋转角α的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1).
(1)继续填写:A6(________,________),A7(________,________),A8(________,________),A9((________,________).A10((________,________),A11(________,________),A12(________,________),A13(________,________).
(2)写出点A2010(________,________),A2011(________,________).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,点P在矩形ABCD内.若AB=4cm,BC=6cm,AE=CG=3cm,BF=DH=4cm,四边形AEPH的面积为5cm2,则四边形PFCG的面积为_______cm2.
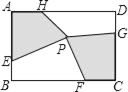
-
科目: 来源: 题型:
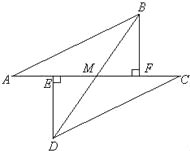
查看答案和解析>>【题目】如图所示,E、F分别为线段AC上的两个点,且DE⊥AC于点E,BF⊥AC于点F,若AB=CD,AE=CF,BD交AC于点M.
(1)试猜想DE与BF的关系,并证明你的结论;
(2)求证:MB=MD.
相关试题

