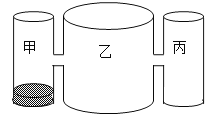
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面面积之比为1:4:1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示,若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm.
cm.
求:(1)开始注水1分钟,丙容器的水位上升了多少?
(2)开始注入多少分钟的水量后,甲与乙的水位高度相差0.5cm?
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() .
.
【解析】试题分析:(1)由甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,注水1分钟,乙的水位上升![]() cm,得到注水1分钟,丙的水位上升
cm,得到注水1分钟,丙的水位上升![]() cm;
cm;
(2)设开始注入t分钟的水量后,乙的水位比甲高0.5cm,有两种情况:①甲的水位不变时,②乙的水位到达管子底部,甲的水位上升时,分别列方程求解即可;设开始注入a分钟的水量后,甲的水位比乙高0.5cm.
试题解析:(1)∵甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,
∵注水1分钟,乙的水位上升![]() cm,
cm,
∴得到注水1分钟,丙的水位上升![]() cm×4=
cm×4=![]() cm;
cm;
(2)设开始注入t分钟的水量后,乙的水位比甲高0.5cm,有两种情况:
①甲的水位不变时;
由题意得, ![]() t1=0.5,
t1=0.5,
解得:t=![]() ,
,
∵![]() ×
×![]() =6>5,
=6>5,
∴此时丙容器已向乙容器溢水,
∵5÷![]() =
=![]() 分钟,
分钟, ![]() ×
×![]() =
=![]() ,即经过
,即经过![]() 分钟时丙容器的水到达管子底部,乙的水位上升
分钟时丙容器的水到达管子底部,乙的水位上升![]() ,
,
∴![]() +2×
+2×![]() (t
(t![]() )1=0.5,解得:t=
)1=0.5,解得:t=![]() ;
;
②当乙的水位到达管子底部,甲的水位上升时,
∵乙的水位到达管子底部的时间为; ![]() +(5
+(5![]() )÷
)÷![]() ÷2=
÷2=![]() 分钟,
分钟,
∴512×![]() (t
(t![]() )=0.5,
)=0.5,
解得:t=![]() ,
,
综上所述开始注入![]() 或
或![]() 分钟的水量后,乙的水位比甲高0.5cm;
分钟的水量后,乙的水位比甲高0.5cm;
③设开始注入a分钟的水量后,甲的水位比乙高0.5cm,
由题意得:10.5=![]() a,
a,
解得:a=![]()
答:开始注入![]() ,40分钟的水量后,甲与乙的水位高度之差是0.5cm.
,40分钟的水量后,甲与乙的水位高度之差是0.5cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,通过观察,用你所发现的规律确定22011的个位数字是( )
A. 2 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=-1是关于x的方程2x+a=1的解,则a的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?并说明理由;

-
科目: 来源: 题型:
查看答案和解析>>【题目】a、b、c是实数,点A(a+1、b)、B(a+2,c)在二次函数y=x2﹣2ax+3的图象上,则b、c的大小关系是bc(用“>”或“<”号填空)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列说法:①∠ECG和∠C是同一个角;②∠OGF和∠DGB是同一个角;③∠DOF和∠EOG是同一个角;④∠ABC和∠CBD是同一个角.其中正确的说法有( )
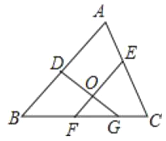
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,
①四边形ACED是平行四边形;
②△BCE是等腰三角形;
③四边形ACEB的周长是10+2 ;
;
④四边形ACEB的面积是16.
则以上结论正确的是( )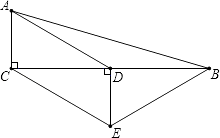
A.①②③
B.①②④
C.①③④
D.②④
相关试题

