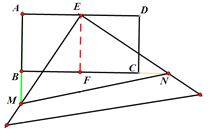
【题目】在矩形ABCD中,AD=2AB=4,E是AD的中点,一块足够大的三角板的直角顶点与点E重合,将三角板绕点E旋转,三角板的两直角边分别交AB,BC(或它们的延长线)于点M,N.
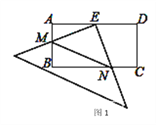
(1)观察图1,直接写出∠AEM与∠BNE的关系是 ;(不用证明)
(2)如图1,当M、N都分别在AB、BC上时,可探究出BN与AM的关系为: ;(不用证明)
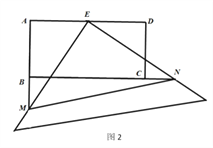
(3)如图2,当M、N都分别在AB、BC的延长线上时,(2)中BN与AM的关系式是否仍然成立?若成立,请说明理由:若不成立,写出你认为成立的结论,并说明理由.
参考答案:
【答案】(1)互余(或∠AEM+∠BNE=90 等);(2)①BN⊥AM ;② BN-AM=2;(3)成立,理由见解析.
【解析】试题分析:(1)由矩形的对边平行,得∠AEM+∠BNE=90 ;
(2)作辅助线EF⊥BC于点F,然后证明Rt△AME≌Rt△FNE,从而得到结论;
(3)成立.
试题解析:(1):互余(或∠AEM+∠BNE=90 等)
(2)①BN⊥AM ;② BN-AM=2
如图,
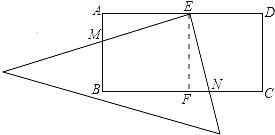
在矩形ABCD中,AD=2AB,E是AD的中点,
作EF⊥BC于点F,则有AB=AE=EF=FC,
∵∠AEM+∠DEN=90°,∠FEN+∠DEN=90°,
∴∠AEM=∠FEN,
在Rt△AME和Rt△FNE中,
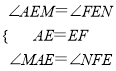
∴Rt△AME≌Rt△FNE,
∴BM=CN,
∵AD=2AB=4,
∴BC=4,AB=2
∴BN-AM=BC-CN-AM=BC-BM-AM=BC-(BM+AM)=BC-AB=4-2=2
(3)当M、N都分别在AB、BC的延长线上时,(2)中BN与AM的关系式仍然成立.
如图,过E作EF⊥BC于F
∵ 矩形ABCD中,AD=2AB=4,E是AD的中点
∴AE=EF=AB=BF=2
∵ ∠AEM+∠MEF=90 ,∠NEF+∠MEF=90
∴∠AEM=∠NEF
∴ Rt△AEM≌ Rt△FEN
∴AM=FN
∴BN-AM= BN-FN=BF= 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+mx﹣8=0的一个实数根为2,则另一实数根及m的值分别为( )
A.4,﹣2
B.﹣4,﹣2
C.4,2
D.﹣4,2 -
科目: 来源: 题型:
查看答案和解析>>【题目】现定义运算“★”,对于任意实数a、b,都有a★b=a2﹣3a+b.如:3★5=32﹣3×3+5,若x★2=6,试求实数x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+
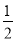 x+c经过B、C两点,点E是直线BC上方抛物线上的一动点.
x+c经过B、C两点,点E是直线BC上方抛物线上的一动点.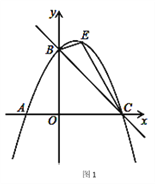
(1)求抛物线的解析式;
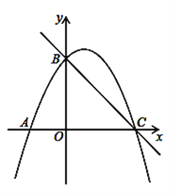
(2)过点E作y轴的平行线交直线BC于点M、交x轴于点F,当S△BEC=
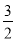 时,请求出点E和点M的坐标;
时,请求出点E和点M的坐标;(3)在(2)的条件下,当E点的横坐标为1时,在EM上是否存在点N,使得△CMN和△CBE相似?如果存在,请直接写出点N的坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写如表:

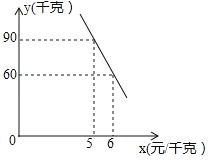
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】由几个相同的边长为1的小立方块搭成的几何体的俯视图如图所示.方格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个几何体的正视图和左视图.
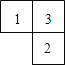
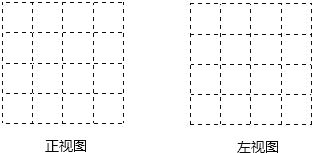
(2)根据三视图,请你求出这个组合几何体的表面积(包括底面积).
-
科目: 来源: 题型:
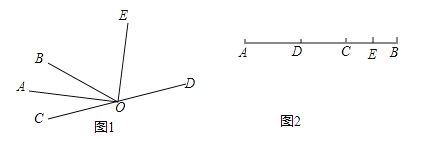
查看答案和解析>>【题目】(1)如图1,已知O是直线CD上的点,OA平分∠BOC,OE平分∠BOD,∠AOC=35°,求∠BOE,∠COE的度数.
(2)如图2,已知AB=16cm,C是AB上一点,点D是线段AC的中点,点E是线段BC的中点,求线段DE的长度.
相关试题

