搜索
【题目】整式与方程
(1)先化简，再求值：3x2y﹣[2x2y﹣3(2xy﹣x2y)﹣xy]，其中x＝﹣1，y＝﹣2．
(2)解方程：
①4﹣x＝3(2﹣x)
②
＝3+
参考答案：
【答案】(1)﹣2x2y+7xy；18；(2)①x＝1；②x＝4．
【解析】
(1)先去掉括号，然后合并同类项，再把x、y的值代入进行计算即可得解．
(2)根据去分母、去括号，再移项，合并同类项，把x的系数化为1解答即可．
解：(1)原式＝3x2y﹣2x2y+6xy﹣3x2y+xy
＝﹣2x2y+7xy，
把x＝﹣1，y＝﹣2代入﹣2x2y+7xy＝﹣2×(﹣1)2×(﹣2)+7×(﹣1)×(﹣2)＝18；
(2)①4﹣x＝6﹣3x
﹣x+3x＝6﹣4
2x＝2
x＝1；
②2(x+1)＝12+x﹣6
2x+2＝12+x﹣6
2x﹣x＝12﹣6﹣2
x＝4．
-
科目： 来源： 题型：
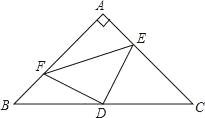
查看答案和解析>>【题目】已知：如图，Rt△ABC中，∠BAC＝90°，AB＝AC，D是BC的中点，AE＝BF．若BC＝8，则四边形AFDE的面积是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】列方程解应用题：
有一些相同的房间需要粉刷，一天 3名一级技工去粉刷 8个房间，结果其中有 50
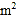墙面未来得及刷；同样时间内 5名二级技工粉刷了 10个房间之外，还多刷了另外的40 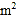墙面．已知每名同级别的技工每天的工作效率相同，每名一级技工比二级技工每天多刷 10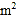墙面，求每个一级技工和二级技工每天粉刷的墙面各是多少平方米? -
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，已知线段AB=12cm，点C为线段AB上的一个动点，点D、E分别是AC和BC的中点．
（1）若点C恰好是AB的中点，则DE= cm；若AC=4cm，则DE= cm；
（2）随着C点位置的改变，DE的长是否会改变？如果改变，请说明原因；如果不变，请求出DE的长；
（3）知识迁移：如图②，已知∠AOB=120°，过角的内部任意一点C画射线OC，若OD、OE分别平分∠AOC和∠BOC，试说明∠DOE的度数与射线OC的位置无关．
-
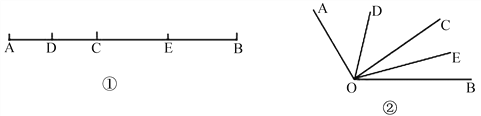
科目： 来源： 题型：
查看答案和解析>>【题目】我市某蔬菜种植农户购买白菜苗和西红柿苗共1000株，其中白菜苗每株3元，西红柿苗每株5元．已知该农户打算用不少于3600元但不多于3800元的资金购买两种蔬菜．
（1）求该农户可以购买白菜苗株数的最大值和最小值；
（2）该农户按（1）中购买白菜苗株数的最小值的方案购买两种蔬菜苗，经过农户的精心培育，两种蔬菜苗全成活．根据以往的数据分析，平均一株白菜苗可长成2千克白菜，平均一株西红柿苗可结3千克西红柿．农户计划采用直接销售和生态采摘销售两种方式进行销售，其中直接销售白菜的售价为每千克4元，直接销售西红柿的售价为每千克5元；生态采摘销售时两种蔬菜的售价一样，都比直接销售白菜的售价高
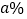，但生态采摘过程中会有
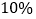的损耗．当白菜和西红柿各直接销售一半后、剩下的全部采用生态采摘销售时，该农户可获得8080元的利润．求
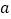的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】某中学广场上有旗杆如图1所示，在学习解直角三角形以后，数学兴趣小组测量了旗杆的长度．如图2，在某一时刻，光线与水平面的夹角为72°，旗杆AB的影子一部分落在平台上，另一部分落在斜坡上，测得落在平台上的影长BC为4米，落在斜坡上的影长CD为3米，AB⊥BC，同一时刻，若1米的竖立标杆PQ在斜坡上的影长QR为2米，求旗杆AB的长度．（结果精确到0.1米．参考数据：sin72°≈0.95，cos72°≈0.31，tan72°≈3.08）．
-
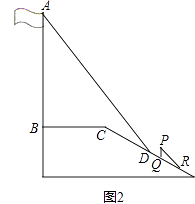
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：
如图①，图形l外一点P与图形l上各点连接的所有线段中，若线段PA1最短，则线段PA1的长度称为点P到图形l的距离．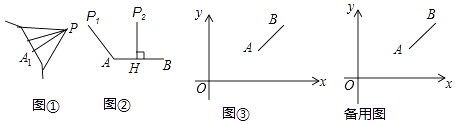
例如：图②中，线段P1A的长度是点P1到线段AB的距离；线段P2H的长度是点P2到线段AB的距离．
解决问题：
如图③，平面直角坐标系xOy中，点A、B的坐标分别为（8，4），（12，7），点P从原点O出发，以每秒1个单位长度的速度向x轴正方向运动了t秒．
（1）当t=4时，求点P到线段AB的距离；
（2）t为何值时，点P到线段AB的距离为5？
（3）t满足什么条件时，点P到线段AB的距离不超过6？（直接写出此小题的结果）
相关试题
