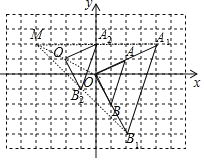
【题目】如图11,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,-2),P(a,b)是△OAB的边AB上一点.
(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1 ,使它与△OAB的相似比为2:1,并分别写出点A、P的对应点A1、P1的坐标;
(2)画出将△OAB向左平移2个单位,再向上平移1个单位后的△O2A2B2 ,并写出点A、P的对应点A2、P2的坐标;
(3)判断△OA1B1与△O2A2B2 ,能否是关于某一点M为位似中心的位似图形,若是,请在图11中标出位似中心M,并写出点M的坐标.

参考答案:
【答案】(1)A1(4,2),P1(2a,2b) (2)A2(0,2),P2(a-2,b+1)(3)△OA1B1与△O2A2B2是关于点M(-4,2)为位似中心的位似图形
【解析】试题分析: (1)分别延长![]() 使
使![]() 则
则
![]() 满足条件,然后写出点
满足条件,然后写出点![]() 的坐标;
的坐标;
(2)利用点平移的坐标规律写出![]() 的坐标,然后描点即可;
的坐标,然后描点即可;
(3)延长![]() 它们相交于一点,则可判定
它们相交于一点,则可判定![]() 和
和![]() 是位似图形,然后写交点坐标.
是位似图形,然后写交点坐标.
试题解析:如图, ![]() 为所作,点
为所作,点![]() 的坐标分别为
的坐标分别为![]()
(2)如图, ![]() 为所作,点
为所作,点![]() 的坐标分别为
的坐标分别为![]()
(3)如图: ![]() 和
和![]() 是位似图形,,如图,点M为所,位似中心M的坐标为
是位似图形,,如图,点M为所,位似中心M的坐标为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C, D为OC的中点,直线AD交抛物线于点E(2,6),且△ABE与△ABC的面积之比为3∶2.

(1)求这条抛物线对应的函数关系式;
(2)连结BD,试判断BD与AD的位置关系,并说明理由;
(3)连结BC交直线AD于点M,在直线AD上,是否存在这样的点N(不与点M重合),使得以A、B、N为顶点的三角形与△ABM相似?若存在,请求出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块矩形纸板,长为20cm,宽为14cm,在它的四角各切去一个同样的正方形,然后将四周突出部分沿虚线折起,就能制作一个无盖的长方体盒子,如果这个无盖的长方体底面积为160cm2,那么该长方体盒子体积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批小家电,平均每天可售出20台,每台盈利40元.为了去库存,商场决定采取适当的降价措施.经调查发现,在一定范围内,小家电的单价每降5元,商场平均每天可多售出10台.
(1)若将这批小家电的单价降低x元,则每天的销售量是______台(用含x的代数式表示);
(2)如果商场通过销售这批小家电每天要盈利1250元,那么单价应降多少元?
(3)若这批小家电的单价有三种降价方式:降价10元、降价20元、降价30元,如果你是商场经理,你准备采取哪种降价方式?说说理由.
-
科目: 来源: 题型:
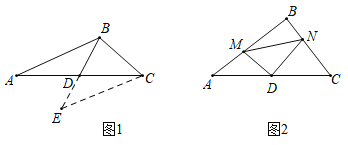
查看答案和解析>>【题目】(1)阅读理解:如图1,在
 中,若
中,若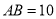 ,
,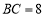 .求
.求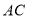 边上的中线
边上的中线 的取值范围.小聪同学是这样思考的:延长
的取值范围.小聪同学是这样思考的:延长 至
至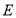 ,使
,使 ,连结
,连结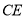 .利用全等将边
.利用全等将边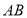 转化到
转化到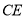 ,在
,在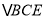 中利用三角形三边关系即可求出中线
中利用三角形三边关系即可求出中线 的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是__________;中线
的取值范围.在这个过程中小聪同学证三角形全等用到的判定方法是__________;中线 的取值范围是__________.
的取值范围是__________.(2)问题解决:如图2,在
 中,点
中,点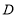 是
是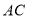 的中点,点
的中点,点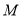 在
在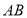 边上,点
边上,点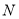 在
在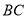 边上,若
边上,若 .求证:
.求证: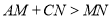 .
.
-
科目: 来源: 题型:
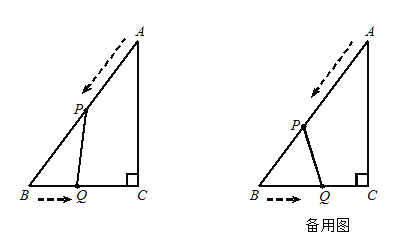
查看答案和解析>>【题目】如图12,在△ABC中,∠C=90°,AB=10cm,BC=6cm. 点P从点A出发,沿AB边以2 cm/s的速度向点B匀速移动;点Q从点B出发,沿BC边以1 cm/s的速度向点C匀速移动. 当一个运动点到达终点时,另一个运动点也随之停止运动,设运动的时间为t(s).
(1)当PQ∥AC时,求t的值;
(2)当t为何值时,QB=QP;
(3)当t为何值时,△PBQ的面积等于4.8cm 2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)(-16
 )-(-10
)-(-10 )-(1
)-(1 );(2)(-8)×(-4)-80÷(-6)
);(2)(-8)×(-4)-80÷(-6)(3)—|
 |—|-
|—|- ×
× |—|—3|;(4)18+32÷(-2)2—(—4)2×5
|—|—3|;(4)18+32÷(-2)2—(—4)2×5
相关试题

