搜索
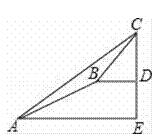
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动，如图，在点A处测得直立于地面的大树顶端C的仰角为36°，然后沿在同一剖面的斜坡AB行走13米至坡顶B处，然后再沿水平方向行走6米至大树脚底点D处，斜面AB的坡度（或坡比）i=1：2.4，求大树CD的高度？（参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73）
参考答案：
【答案】8.1米
【解析】试题分析：作BF⊥AE于F，则FE=BD=6米，DE=BF，设BF=x米，则AF=2.4米，在Rt△ABF中，由勾股定理得出方程，解方程求出DE=BF=5米，AF=12米，得出AE的长度，在Rt△ACE中，由三角函数求出CE，即可得出结果．
试题解析：解：作BF⊥AE于F，如图所示，则FE=BD=6米，DE=BF．∵斜面AB的坡度i=1：2.4，∴AF=2.4BF．设BF=x米，则AF=2.4x米．在Rt△ABF中，由勾股定理得： 
，解得：x=5，∴DE=BF=5米，AF=12米，∴AE=AF+FE=18米．在Rt△ACE中，CE=AEtan36°=18×0.73=13.14米，∴CD=CE﹣DE=13.14米﹣5米≈8.1米．
答：大树CD的高度约为8.1米．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某烤鸭店在确定烤鸭的烤制时间时，主要依据的是下表的数据：
鸭的质量/千克
0．5
1
1．5
2
2．5
3
3．5
4
烤制时间/分
40
60
80
100
120
140
160
180
设鸭的质量为x千克，烤制时间为t分钟，估计当
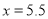时，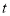
的值为（ ）A. 140B. 200C. 240D. 260
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
和
中，
，还需再添加两个条件才能使
，则不能添加的一组条件是（ ）
A. AC=DE，∠C=∠EB. BD=AB，AC=DE
C. AB=DB，∠A=∠DD. ∠C=∠E，∠A=∠D
-
科目： 来源： 题型：
查看答案和解析>>【题目】在
中，
，
的垂直平分线与
所在直线相交所得的锐角为
则底角
的大小为__________． -
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂计划生产
、
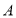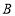两种产品共60件，需购买甲、乙两种材料，生产一件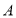产品需甲种材料4千克，乙种材料1千克；生产一件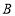产品需甲、乙两种材料各3千克，经测算，购买甲、乙两种材料各1千克共需资金60元；购买甲种材料2千克和乙种材料3千克共需资金155元．（1）甲、乙两种材料每千克分别是多少元？
（2现工厂用于购买甲、乙两种材料的资金不超过9900元，且生产
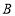产品不少于38件，问符合生产条件的生产方案有哪几种？（3）在（2）的条件下，若生产一件
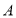产品需加工费40元，若生产一件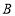产品需加工费50元，应选择哪种生产方案，使生产这60件产品的成本最低？（成本=材料费+加工费） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形
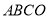的边
、
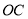在坐标轴上，点
坐标
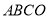，将正方形绕点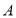
顺时针旋转角度
，得到正方形
，
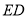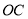交线段于点
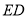，的延长线交线段
于点
，连
、
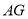．（1）求证：
； （2）求
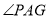的度数，并判断线段
、
、
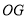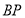之间的数量关系，说明理由；（3）当
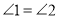时，求直线
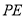的解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某林业部门要考察某种幼树在一定条件下的移植成活率，下图是这种幼树在移植过程中成活情况的一组数据统计结果．下面三个推断：①当移植棵数是1500时，该幼树移植成活的棵数是1356，所以“移植成活”的概率是0．904；②随着移植棵数的增加，“移植成活”的频率总在0．880附近摆动，显示出一定的稳定性，可以估计这种幼树“移植成活”的概率是0．880；③若这种幼树“移植成活”的频率的平均值是0．875，则“移植成活”的概率是0．875．其中合理的是（ ）
A. ①③B. ②③C. ①D. ②
相关试题
