【题目】如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.
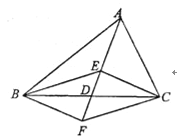
(1)求证:△BDF≌△CDE;
(2)若AB=AC,求证:四边形BFCE是菱形.
参考答案:
【答案】(1)△BDF≌△EDC;(2)四边形BFCE是菱形.
【解析】试题分析:(1)由CE、BF的内错角相等,可得出△CED和△BFD的两组对应角相等;已知D是BC的中点,即BD=DC,由AAS即可证得两三角形全等;
(2)若AB=AC,则△ABC是等腰三角形,而D是底边BC的中点,根据等腰三角形三线合一的性质可证得AD⊥BC;由(1)的全等三角形,易证得四边形BFCE的对角线互相平分;根据对角线互相垂直平分的四边形是菱形即可判定四边形BFCE是菱形.
试题解析:(1)∵CE∥BF,
∴∠ECD=∠FBD,∠DEC=∠DFB;
又∵D是BC的中点,即BD=DC,
∴△BDF≌△EDC(AAS)
(2)∵AB=AC,
∴△ABC是等腰三角形;
又∵BD=DC,∴AD⊥BC(三线合一),
由(1)知:△BDF≌△EDC,
则DE=DF,DB=DC;
∴四边形BFCE是菱形(对角线互相平分且互相垂直的四边形为菱形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算a6b2÷(ab)2的结果是( )
A.a3
B.a4
C.a3b
D.a4b -
科目: 来源: 题型:
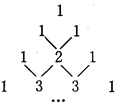
查看答案和解析>>【题目】如图是我国古代数学家杨辉最早发现的图形,称为“杨辉三角”.他的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如其中每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2,展开式中的系数1、2、1恰好对应图中第三行的数字;再如,(a+b)3=a3+3a2b+3ab2+b3,展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出(a+b)4的展开式,(a+b)4=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读材料,再解答下列问题:
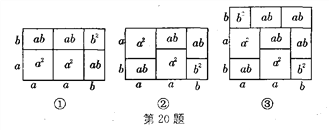
我们已经知道,多项式与多项式相乘的法则可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示.例如:(2a+b) (a+b)=2a2+3ab+b2就可以用图①或图②等图形的面积来表示.
(1)请写出图③所表示的代数恒等式:
(2)画出一个几何图形,使它的面积能表示(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
(3)请仿照上述方法写出另一个含a、b的代数恒等式,并画出与之对应的几何图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数
100
200
300
500
800
1000
3000
摸到白球的次数
65
124
178
302
481
599
1803
摸到白球的频率
0.65
0.62
0.593
0.604
0.601
0.599
0.601
(1)请估计:当
 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)(2)假如你摸一次,你摸到白球的概率P(白球)= .
(3)试估算盒子里黑、白两种颜色的球各有多少只?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形
 中,
中,  ∥
∥ ,∠
,∠ =90°,
=90°, =28cm,
=28cm,  =24cm,
=24cm, 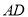 =4cm,点
=4cm,点 从点
从点 出发,以1cm/s的速度向点
出发,以1cm/s的速度向点 运动,点
运动,点 从点
从点 同时出发,以2cm/s的速度向点
同时出发,以2cm/s的速度向点 运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动。则四边
运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动。则四边 的面积
的面积 (cm2)与两动点运动的时间
(cm2)与两动点运动的时间 (s)的函数图象大致是( )
(s)的函数图象大致是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算2x2÷x3的结果是( )
A.x
B.2x
C.x-1
D. 2x-1
相关试题

